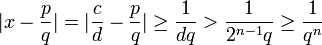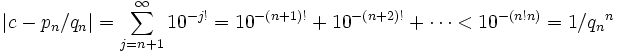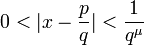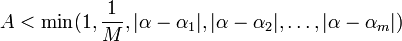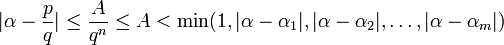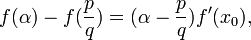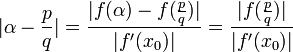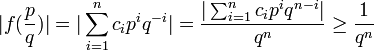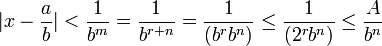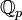- Nombre De Liouville
-
Nombre de Liouville
En théorie des nombres, un nombre de Liouville est un nombre réel x avec la propriété suivante : pour tout nombre entier positif n, il existe des entiers p et q avec
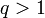 et tels que
et tels que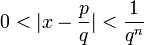 .
.
Un nombre de Liouville peut ainsi être approché « de manière très fine » par une suite de nombres rationnels. En 1844, Joseph Liouville montra que tous les nombres vérifiant l'inégalité ci-dessus sont transcendants, établissant ainsi pour la première fois l'existence de tels nombres.
Sommaire
Irrationalité des nombres de Liouville
Remarquons d'abord que si x est un nombre de Liouville, pour tout nombre entier positif n, il existe alors un nombre infini de paires d'entiers (p,q) obéissant à l'inégalité ci-dessus : il suffit en effet de prendre des couples (p,q) associés à des entiers m égaux à kn , ils fournissent k couples
 associés à n car
associés à n car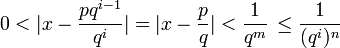 .
.
Il est relativement facile de démontrer que si x est un nombre de Liouville, alors x est un nombre irrationnel. Supposons le contraire ; alors il existe des entiers c, d avec . Soit n un entier positif tel que
. Soit n un entier positif tel que 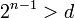 . Alors, il existerait deux entiers p et q tels que
. Alors, il existerait deux entiers p et q tels que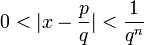 .
.
La première partie de l'inégalité prouve que
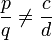 , donc
, doncce qui contredit la définition .
Constante de Liouville
La constante de Liouville est le réel défini par
La constante de Liouville est un nombre de Liouville ; si nous définissons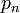 et
et 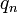 comme suit :
comme suit :alors, pour tous les entiers positifs n, nous avons
La constante de Liouville est le premier exemple de nombre réel dont on a prouvé la transcendance. La fraction continue est l'outil auquel pense Liouville pour construire des nombres de Liouville et donc transcendants. L'article associé présente un autre exemple de cette nature, illustrant la méthode préconisée par le mathématicien.
Mesure irrationnelle d'un réel
La mesure irrationnelle d'un nombre réel x mesure la manière d'approcher un nombre par des rationnels. À la place de n'importe quel n permis pour la puissance de q, nous trouvons la borne supérieure de l'ensemble de nombres réels
 tels que la propriété
tels que la propriétésoit satisfaite par un nombre infini de paires d'entiers (p, q) avec q > 0. Pour toute valeur
 inférieure à cette borne supérieure, l'ensemble de tous les rationnels
inférieure à cette borne supérieure, l'ensemble de tous les rationnels 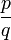 satisfaisant l'inégalité ci-dessus est une approximation fine de x; réciproquement, si
satisfaisant l'inégalité ci-dessus est une approximation fine de x; réciproquement, si  est plus grand que la borne supérieure, alors il n'existe pas de telles suites qui convergent finement vers x.
est plus grand que la borne supérieure, alors il n'existe pas de telles suites qui convergent finement vers x.Les nombres de Liouville sont précisément les nombres ayant une mesure irrationnelle infinie.
Transcendance des nombres de Liouville
En 1844, Joseph Liouville montra que les nombres avec cette propriété ne sont pas seulement irrationnels, mais sont toujours transcendants (voir la démonstration ci-dessous). Il utilisa ce résultat pour fournir le premier exemple explicite de nombre transcendant: la constante de Liouville définie plus haut.
En revanche, bien que chaque nombre de Liouville soit transcendant, tout nombre transcendant n'est pas un nombre de Liouville. Il a été démontré que
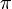 est transcendant, mais pas un nombre de Liouville.
est transcendant, mais pas un nombre de Liouville.La démonstration procède en établissant premièrement la propriété des nombres algébriques irrationnels. Cette propriété dit essentiellement que les nombres algébriques irrationnels ne peuvent pas être approchés correctement par les nombres rationnels. Un nombre de Liouville est irrationnel mais n'a pas cette propriété, donc il ne peut pas être algébrique et doit être transcendant. Le lemme suivant est connu habituellement comme le théorème de Liouville (sur l'approximation diophantienne), il existe plusieurs résultats connus comme le théorème de Liouville.
Lemme : Si
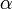 est un nombre irrationnel qui est la racine d'un polynôme f de degré n > 0 à coefficients entiers, alors il existe un nombre réel A > 0 tel que, pour tous les entiers p, q, avec q > 0,
est un nombre irrationnel qui est la racine d'un polynôme f de degré n > 0 à coefficients entiers, alors il existe un nombre réel A > 0 tel que, pour tous les entiers p, q, avec q > 0, .
.
Démonstration du lemme
Soit M, la valeur maximale de
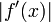 sur l'intervalle
sur l'intervalle ![[\alpha-1, \alpha+1]\,](/pictures/frwiki/99/c3af89894ab8bdde9fb6db63e39f5ccc.png) . Soit
. Soit 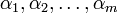 les racines distinctes de f qui diffèrent de
les racines distinctes de f qui diffèrent de 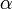 . Prenons une certaine valeur
. Prenons une certaine valeur 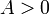 satisfaisant
satisfaisantMaintenant, supposons qu'il existe certains entiers p, q contredisant le lemme. Alors
Alors
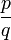 est dans l'intervalle
est dans l'intervalle ![[\alpha - 1, \alpha + 1]\,](/pictures/frwiki/99/c3af89894ab8bdde9fb6db63e39f5ccc.png) ; et
; et 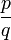 n'est pas dans
n'est pas dans 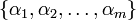 , et comme
, et comme 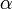 est irrationnel,
est irrationnel, 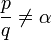 donc
donc 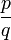 n'est pas une racine de f.
n'est pas une racine de f.Par le théorème des accroissements finis, il existe un
 entre
entre 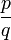 et
et 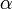 tel que
tel quePuisque
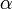 est une racine de f mais
est une racine de f mais 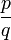 ne l'est pas, nous voyons que
ne l'est pas, nous voyons que  et nous pouvons réordonner :
et nous pouvons réordonner :Maintenant, f est de la forme
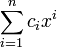 où chaque
où chaque 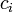 est un entier ; donc nous pouvons exprimer
est un entier ; donc nous pouvons exprimer 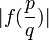 comme
commela dernière inégalité reste valable parce que
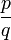 n'est pas une racine de f.
n'est pas une racine de f.Ainsi, nous avons
 . Puisque
. Puisque  par la définition de M, et
par la définition de M, et 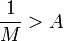 par la définition de A, nous avons
par la définition de A, nous avonsce qui est une contradiction; par conséquent, aucun p, q n'existe; ce qui démontre le lemme.
Démonstration de l'assertion
Comme conséquence de ce lemme, soit x un nombre de Liouville ; comme noté dans le texte de l'article, x est alors irrationnel. Si x est algébrique, alors par le lemme, il existe un certain entier n et un certain réel positif A tel que pour tous les p, q
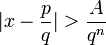 .
.
Soit r un entier positif tel que
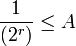 . Soit m = r + n, alors, puisque x est un nombre de Liouville, il existe des entiers a, b > 1 tel que
. Soit m = r + n, alors, puisque x est un nombre de Liouville, il existe des entiers a, b > 1 tel quece qui contredit le lemme ; par conséquent x n'est pas algébrique, et est ainsi transcendant.
Théorème d'Erdös
Paul Erdös a démontré [1] en 1962 que tout nombre réel pouvait s'écrire comme somme ou comme produit de deux nombres de Liouville
Annexes
Notes et références
Voir aussi
Lien externe
- Article du 13 mai 1844 de Liouville sur les nombres transcendants (accès à l'article et analyse de M. Mendès-France, mathématicien) (site BibNum)
- Le commencement des nombres transcendants (en anglais)
- Portail des mathématiques
Catégories : Nombre transcendant | Propriété numérique | Approximation diophantienne
Wikimedia Foundation. 2010.