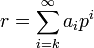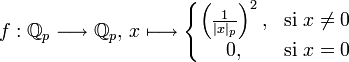- Nombre P-Adique
-
Nombre p-adique
En théorie des nombres, si p est un nombre premier, un nombre p-adique est un objet mathématique qui peut se concevoir comme une suite de chiffres en base p, éventuellement infinie à gauche de la virgule (mais toujours finie à droite de la virgule). Avec une addition et une multiplication qui se calculent comme pour les nombres décimaux usuels, l'ensemble des nombres p-adiques forme un corps noté
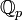 . Un nombre 2-adique est parfois appelé « diadique » mais ne doit pas être confondu avec une fraction dyadique. Un nombre 3-adique est parfois appelé « triadique ».
. Un nombre 2-adique est parfois appelé « diadique » mais ne doit pas être confondu avec une fraction dyadique. Un nombre 3-adique est parfois appelé « triadique ».Chaque corps
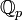 des nombres p-adiques est construit par complétion du corps
des nombres p-adiques est construit par complétion du corps 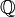 des nombres rationnels lorsque celui-ci est muni d'une norme particulière nommée norme p-adique. Cette construction s'apparente à celle du corps
des nombres rationnels lorsque celui-ci est muni d'une norme particulière nommée norme p-adique. Cette construction s'apparente à celle du corps  des nombres réels par complétion du corps des rationnels suivant la valeur absolue.
des nombres réels par complétion du corps des rationnels suivant la valeur absolue.La principale motivation ayant donné naissance aux corps des nombres p-adiques était de pouvoir utiliser les techniques des séries entières dans la théorie des nombres, mais leur utilité dépasse maintenant largement ce cadre. De plus, la norme p-adique sur le corps
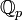 est une norme non-archimédienne : on obtient sur ce corps une analyse différente de l'analyse usuelle sur les réels, que l'on appelle analyse p-adique.
est une norme non-archimédienne : on obtient sur ce corps une analyse différente de l'analyse usuelle sur les réels, que l'on appelle analyse p-adique.Sommaire
Construction
Approche analytique
Les nombres réels sont définis comme des classes d'équivalence des suites de Cauchy des nombres rationnels. Cependant, cette définition repose sur la métrique choisie et, en en choisissant une autre, d'autres nombres que les nombres réels peuvent être construits. La métrique utilisée pour les nombres réels est appelée métrique euclidienne.
Pour un nombre premier donné p, on définit la norme p-adique sur
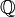 comme suit :
comme suit :- on appelle valuation p-adique d'un entier a non nul (et l'on note vp(a)) l'exposant de p dans la décomposition de a en produit de facteurs premiers.
- on peut alors construire une valuation pour tout nombre rationnel non nul en posant :
 .
.
- On prouve aisément que cette définition est indépendante du représentant du rationnel choisi.
- La norme p-adique | r | p d'un rationnel r non nul vaut
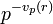 .
. - Si r est nul, on pose | r | p = 0. Ce prolongement est compatible avec l'idée que 0 est divisible par pk pour toute valeur de k, donc que la valuation de 0 serait infinie.
En quelque sorte, plus r est divisible par p, plus sa norme p-adique est petite (c'est un cas particulier de valuation discrète, un outil algébrique).
Par exemple, pour
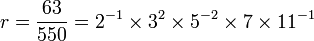 :
: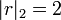

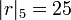
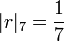
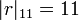
 pour tout autre nombre premier.
pour tout autre nombre premier.
On démontre que cette application a toutes les propriétés d'une norme. On peut montrer que toute norme (non-triviale) sur
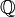 est équivalente soit à la norme euclidienne, soit à une norme p-adique (théorème d'Ostrowski). Une norme p-adique définit une métrique dp sur
est équivalente soit à la norme euclidienne, soit à une norme p-adique (théorème d'Ostrowski). Une norme p-adique définit une métrique dp sur  en posant :
en posant :- dp(x,y) = | x − y | p
Le corps
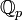 des nombres p-adiques peut alors être défini comme la complétion de l'espace métrique (
des nombres p-adiques peut alors être défini comme la complétion de l'espace métrique (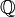 , dp). Ses éléments sont les classes d'équivalences des suites de Cauchy, où deux suites sont dites équivalentes si leur différence converge vers zéro. De cette façon, on obtient un espace métrique complet qui est aussi un corps et qui contient
, dp). Ses éléments sont les classes d'équivalences des suites de Cauchy, où deux suites sont dites équivalentes si leur différence converge vers zéro. De cette façon, on obtient un espace métrique complet qui est aussi un corps et qui contient 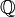 .
.Cette construction permet de comprendre pourquoi
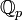 est un analogue arithmétique de
est un analogue arithmétique de 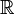 .
.Approche algébrique
Dans cette approche algébrique, on commence par définir l'anneau des entiers p-adiques, puis par construction le corps des fractions de cet anneau pour obtenir le corps des nombres p-adiques.
On définit l'anneau des entiers p-adiques
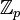 comme la limite projective des anneaux
comme la limite projective des anneaux  . Un entier p-adique est alors une suite
. Un entier p-adique est alors une suite  telle que
telle que  et que, si n < m, an = am[pn].
et que, si n < m, an = am[pn].Par exemple, 35 en tant que nombre 2-adique serait la suite
 .
.L'addition et la multiplication de telles suites sont bien définies, puisqu'elles commutent avec l'opérateur modulo (voir arithmétique modulaire). De plus, toute suite (an) dont le premier élément n'est pas nul a un inverse.
L'anneau des entiers p-adiques ne possédant pas de diviseurs de zéro, il est possible de considérer son corps des fractions pour obtenir le corps
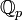 des nombres p-adiques.
des nombres p-adiques.Décomposition canonique de Hensel
Soit p un nombre premier. Tout élément non nul r de
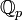 (et en particulier tout élément de
(et en particulier tout élément de 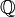 ) s'écrit de manière unique sous la forme :
) s'écrit de manière unique sous la forme :où
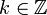 et les ai sont des nombres entiers compris entre 0 et p − 1. Cette écriture est la décomposition canonique de r comme nombre p-adique.
et les ai sont des nombres entiers compris entre 0 et p − 1. Cette écriture est la décomposition canonique de r comme nombre p-adique.Cette série est convergente suivant la métrique p-adique.
On note
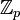 l'ensemble des éléments de
l'ensemble des éléments de 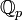 tels que
tels que 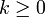 et on l'appelle ensemble des entiers p-adiques.
et on l'appelle ensemble des entiers p-adiques. 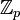 est un sous-anneau de
est un sous-anneau de 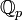 . On peut représenter un entier p-adique par une suite infinie vers la gauche de chiffres en base p, tandis que les autres éléments de
. On peut représenter un entier p-adique par une suite infinie vers la gauche de chiffres en base p, tandis que les autres éléments de 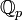 , eux, auront un nombre fini de chiffres à droite de la virgule. Cette écriture fonctionne en somme à l'inverse de ce qu'on a l'habitude de rencontrer dans l'écriture des nombres réels.
, eux, auront un nombre fini de chiffres à droite de la virgule. Cette écriture fonctionne en somme à l'inverse de ce qu'on a l'habitude de rencontrer dans l'écriture des nombres réels.Par exemple, avec p = 2 :
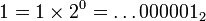 (le 2 en indice indiquant qu'il s'agit du développement 2-adique de 1)
(le 2 en indice indiquant qu'il s'agit du développement 2-adique de 1) : on peut vérifier que, puisque
: on peut vérifier que, puisque 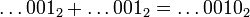 , ajouter 1 à cette écriture conduit à décaler une retenue tout le long de l'écriture, pour finalement donner 0.
, ajouter 1 à cette écriture conduit à décaler une retenue tout le long de l'écriture, pour finalement donner 0.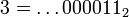
 : en multipliant ce résultat par
: en multipliant ce résultat par 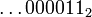 , on retrouve 1.
, on retrouve 1. représente un élément de
représente un élément de  (et même de
(et même de 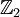 ) qui n'est pas dans
) qui n'est pas dans 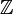 .
.- Le polynôme 2X2 + X + 2 se factorise dans
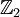 sous la forme (X − a)(2X − b) avec
sous la forme (X − a)(2X − b) avec  et
et 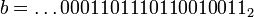 , alors qu'il est irréductible dans
, alors qu'il est irréductible dans 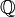 ou
ou  . On a 2a + b = − 1 et ab = 2.
. On a 2a + b = − 1 et ab = 2.
Un autre exemple, avec p = 7 :
2 n'a pas de racine carrée dans
 mais en possède deux dans
mais en possède deux dans 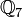 , à savoir :
, à savoir : 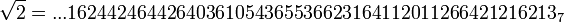 et son opposé :
et son opposé : 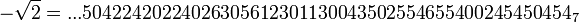
Propriétés
Dénombrabilité
L'ensemble des entiers p-adiques n'est pas dénombrable.
Les nombres p-adiques contiennent les nombres rationnels et forment un corps de caractéristique nulle. Il n'est pas possible d'en faire un corps ordonné.
Topologie
La topologie sur l'ensemble des entiers p-adiques est celle de l'ensemble de Cantor; la topologie sur l'ensemble des nombres p-adiques est celle de l'ensemble de Cantor privé d'un point (qui serait naturellement appelé infini). En particulier, l'espace des entiers p-adiques est compact, tandis que l'espace des nombres p-adiques ne l'est que localement. En tant qu'espaces métriques, les entiers et les nombres p-adiques sont complets.
Les nombres réels n'ont qu'une seule extension algébrique propre, les nombres complexes. En d'autres termes, cette extension quadratique est algébriquement close. En revanche, la clôture algébrique des nombres p-adiques est de degré infini : les corps
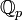 ont une infinité d'extensions algébriques non équivalentes. De plus, la clôture algébrique d'un
ont une infinité d'extensions algébriques non équivalentes. De plus, la clôture algébrique d'un 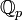 n'est pas complète. Sa complétion métrique est appelée Ωp et elle est algébriquement close.
n'est pas complète. Sa complétion métrique est appelée Ωp et elle est algébriquement close.Le corps Ωp, aussi noté
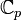 , est abstraitement isomorphe au corps
, est abstraitement isomorphe au corps 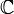 des nombres complexes et il est possible de considérer le premier comme le dernier, muni d'une métrique exotique. Cependant, l'existence d'un tel isomorphisme est une conséquence de l'axiome du choix et il n'est pas possible d'en expliciter un.
des nombres complexes et il est possible de considérer le premier comme le dernier, muni d'une métrique exotique. Cependant, l'existence d'un tel isomorphisme est une conséquence de l'axiome du choix et il n'est pas possible d'en expliciter un.Les nombres p-adiques contiennent le ne corps cyclotomique si et seulement si n divise p − 1. Par exemple, les 1er, 2e, 3e, 4e, 6e et 12e corps cyclotomiques sont des sous-corps de
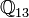 .
.Le nombre e (défini par la série
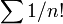 ) n'est élément d'aucun des corps p-adiques. Cependant, ep (défini par la série
) n'est élément d'aucun des corps p-adiques. Cependant, ep (défini par la série  ) est un nombre p-adique (sauf si p = 2, mais e4 est un nombre 2-adique), aussi e, défini comme une racine p-ème de ep, est un élément de la clôture algébrique de tous les corps p-adiques.
) est un nombre p-adique (sauf si p = 2, mais e4 est un nombre 2-adique), aussi e, défini comme une racine p-ème de ep, est un élément de la clôture algébrique de tous les corps p-adiques.Sur les nombres réels, les seules fonctions dont les dérivées sont nulles sont les fonctions constantes. Ceci n'est pas vrai sur les nombres p-adiques. Par exemple, la fonction
possède une dérivée nulle en tous points, mais n'est même pas constante localement en 0.
Si on se donne les éléments
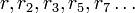 respectivement membres de
respectivement membres de 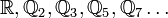 , il est possible de trouver une suite (xn) de
, il est possible de trouver une suite (xn) de 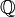 telle que la limite des xn dans
telle que la limite des xn dans  soit r et, pour tout p premier, elle soit rp dans
soit r et, pour tout p premier, elle soit rp dans 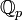 .
.Rationalité
Un nombre positif γ0 est rationnel si, et seulement si, son développement p-adique est périodique à partir d'un certain rang, c'est-à-dire, s'il existe 2 entiers
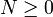 et k > 0 tel que
et k > 0 tel que 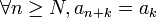 (La suite an représentant le développement p-adique du nombre γ0)
(La suite an représentant le développement p-adique du nombre γ0)Liens internes
- Portail des mathématiques
Catégories : Algèbre | Théorie des nombres | Type de nombre
Wikimedia Foundation. 2010.