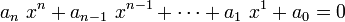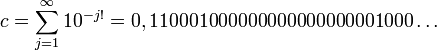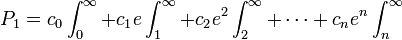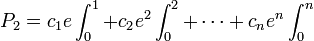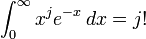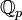- Nombre Transcendant
-
Nombre transcendant
En mathématiques, un nombre transcendant est un nombre réel ou complexe qui n'est racine d'aucune équation polynomiale :
où
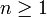 et les coefficients
et les coefficients 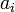 sont des nombres entiers (donc des rationnels), dont au moins l'un an est non nul. Un nombre réel ou complexe est donc transcendant si et seulement s’il n'est pas algébrique.
sont des nombres entiers (donc des rationnels), dont au moins l'un an est non nul. Un nombre réel ou complexe est donc transcendant si et seulement s’il n'est pas algébrique.Les nombres transcendants ne sont jamais rationnels. Néanmoins, tous les nombres irrationnels ne sont pas transcendants : la racine carrée de 2 est irrationnelle, mais est une solution de l'équation polynomiale
 .
.L'ensemble de tous les nombres transcendants est non dénombrable. La preuve est simple : puisque les polynômes à coefficients entiers sont dénombrables, et puisque chacun de ces polynômes possède un nombre fini de zéros, l'ensemble des nombres algébriques est dénombrable. Mais l'argument de la diagonale de Cantor établit que les nombres réels (et par conséquent les nombres complexes aussi) sont non dénombrables, donc l'ensemble de tous les nombres transcendants doit être non dénombrable. En d'autres termes, il y a beaucoup plus de nombres transcendants que de nombres algébriques. Néanmoins, seules peu de classes de nombres transcendants sont connues et prouver qu'un nombre donné est transcendant peut être extrêmement difficile.
Résultats : considérons l'ensemble A des nombres algébriques réels. Alors :
- A est un sous-corps de
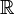 . En particulier, A est stable par addition et multiplication.
. En particulier, A est stable par addition et multiplication. - A est dénombrable, ce qui montre que A est différent de l'ensemble
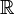 (les nombres transcendants existent bien).
(les nombres transcendants existent bien).
Sommaire
Histoire
Leibniz fut probablement la première personne à croire en l'existence des nombres qui ne satisfont pas les polynômes à coefficients rationnels. Le nom « transcendants » vient de Leibniz dans sa publication de 1682 où il démontra que sin(x) n'est pas une fonction algébrique de x. L'existence des nombres transcendants fut prouvée pour la première fois en 1844 par Joseph Liouville, qui montra des exemples, incluant la constante de Liouville :
dans lequel le n-ième chiffre après la virgule est 1 si n est une factorielle (l'un des nombres 1, 2, 6, 24, 120, 720, etc.) et 0 sinon ; ce nombre est particulièrement bien approché par les nombres rationnels. Joseph Liouville montra que les nombres ayant cette propriété (que nous nommons maintenant nombres de Liouville) sont tous transcendants ; on trouvera cette démonstration à l'article consacré à ces nombres.
Johann Heinrich Lambert, dans son article prouvant l'irrationalité de
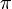 conjectura que
conjectura que  et
et 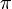 étaient des nombres transcendants. Le premier nombre à avoir été démontré transcendant sans avoir été construit spécialement pour cela fut e, par Charles Hermite en 1873. En 1874, Georg Cantor trouva l'argument décrit ci-dessus établissant l'ubiquité des nombres transcendants.
étaient des nombres transcendants. Le premier nombre à avoir été démontré transcendant sans avoir été construit spécialement pour cela fut e, par Charles Hermite en 1873. En 1874, Georg Cantor trouva l'argument décrit ci-dessus établissant l'ubiquité des nombres transcendants.En 1882, Ferdinand von Lindemann publia une démonstration de la transcendance de
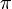 . Il montra d'abord que e à n'importe quelle puissance algébrique non nulle est transcendant, et puisque
. Il montra d'abord que e à n'importe quelle puissance algébrique non nulle est transcendant, et puisque 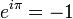 est algébrique (voir identité d'Euler),
est algébrique (voir identité d'Euler), 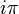 et par conséquent
et par conséquent 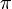 doit être transcendant. Cette approche fut généralisée par Karl Weierstrass avec le théorème de Lindemann-Weierstrass. La transcendance de
doit être transcendant. Cette approche fut généralisée par Karl Weierstrass avec le théorème de Lindemann-Weierstrass. La transcendance de 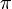 a permis la démonstration de l'impossibilité de plusieurs constructions géométriques anciennes avec le compas et la règle, incluant le plus célèbre d'entre eux, la quadrature du cercle.
a permis la démonstration de l'impossibilité de plusieurs constructions géométriques anciennes avec le compas et la règle, incluant le plus célèbre d'entre eux, la quadrature du cercle.En 1900, David Hilbert a posé une importante question à propos des nombres transcendants, connue sous le nom de septième problème de Hilbert : « Si a est un nombre algébrique non nul et différent de 1 et si b est un nombre algébrique irrationnel, alors le nombre
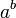 est-il nécessairement transcendant ? » La réponse, affirmative, fut donnée en 1934 par le théorème de Gelfond-Schneider. On peut obtenir facilement des nombres transcendants grâce à lui, par exemple
est-il nécessairement transcendant ? » La réponse, affirmative, fut donnée en 1934 par le théorème de Gelfond-Schneider. On peut obtenir facilement des nombres transcendants grâce à lui, par exemple 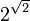 .
.Ce travail fut étendu par Alan Baker dans les années 1960.
Quelques nombres transcendants connus
- Le nombre
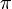 (voir l'article pi).
(voir l'article pi). - Le nombre e (base des logarithmes néperiens)
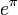 constante de Gelfond
constante de Gelfond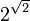 (constante de Gelfond-Schneider) ou plus généralement
(constante de Gelfond-Schneider) ou plus généralement 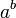 (voir le théorème de Gelfond-Schneider) où
(voir le théorème de Gelfond-Schneider) où  et
et 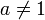 est algébrique et b est algébrique mais non rationnel. Le cas général du septième problème de Hilbert, c’est-à-dire déterminer si
est algébrique et b est algébrique mais non rationnel. Le cas général du septième problème de Hilbert, c’est-à-dire déterminer si 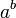 est transcendant lorsque
est transcendant lorsque  et
et 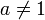 est algébrique et b est irrationnel, reste non résolu.
est algébrique et b est irrationnel, reste non résolu.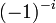 (qui est le nombre réel eπ) pour la raison exposée ci-dessus.
(qui est le nombre réel eπ) pour la raison exposée ci-dessus.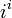 qui est le nombre réel e − π / 2.
qui est le nombre réel e − π / 2.- La valeur de la fonction trigonométrique
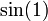
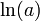 si a est un rationnel strictement positif et différent de 1.
si a est un rationnel strictement positif et différent de 1. ,
, 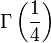 et
et 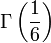 (voir fonction Gamma d'Euler).
(voir fonction Gamma d'Euler).- Le nombre de Champernowne 0,12345678910111213… obtenu en écrivant à la suite les nombres entiers en base dix (théorème de Mahler, 1961)
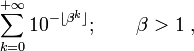
- où
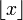 est la partie entière de
est la partie entière de 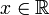 . Par exemple, si
. Par exemple, si  , ce nombre est 0,11010001000000010000000000000001000…
, ce nombre est 0,11010001000000010000000000000001000…
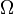 , constante de Chaitin, et plus généralement : chaque nombre non-calculable est transcendant (puisque tous les nombres algébriques sont calculables).
, constante de Chaitin, et plus généralement : chaque nombre non-calculable est transcendant (puisque tous les nombres algébriques sont calculables).
Toute fonction algébrique non constante à une variable donne une valeur transcendante lorsqu'on lui applique une valeur transcendante. Donc, par exemple, en sachant que
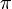 est transcendant, nous pouvons immédiatement déduire que
est transcendant, nous pouvons immédiatement déduire que 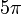 ,
, 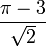 ,
,  et
et 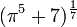 sont aussi transcendants.
sont aussi transcendants.Néanmoins, une fonction algébrique à plusieurs variables peut donner un nombre algébrique lorsqu'elle est appliquée aux nombres transcendants si ces nombres ne sont pas algébriquement indépendants. Par exemple,
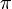 et
et  sont tous les deux transcendants, mais
sont tous les deux transcendants, mais 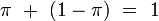 ne l'est évidemment pas. On ignore si
ne l'est évidemment pas. On ignore si  , par exemple est transcendant, mais au moins l'un des deux nombres
, par exemple est transcendant, mais au moins l'un des deux nombres  et
et  doit être transcendant. Plus généralement, pour deux nombres transcendants a et b, au moins l'un de a+b et a b doit être transcendant. Pour voir cela, considérons le polynôme
doit être transcendant. Plus généralement, pour deux nombres transcendants a et b, au moins l'un de a+b et a b doit être transcendant. Pour voir cela, considérons le polynôme 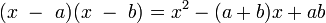 ; si (a+b) et a b étaient tous deux algébriques, alors ce polynôme serait à coefficients algébriques. Comme les nombres algébriques forment un corps algébriquement clos, ceci impliquerait que les racines du polynôme, a et b soient algébriques. Mais ceci est une contradiction et ainsi, au moins un des deux coefficients est transcendant.
; si (a+b) et a b étaient tous deux algébriques, alors ce polynôme serait à coefficients algébriques. Comme les nombres algébriques forment un corps algébriquement clos, ceci impliquerait que les racines du polynôme, a et b soient algébriques. Mais ceci est une contradiction et ainsi, au moins un des deux coefficients est transcendant.Problèmes ouverts
Les nombres dont on ignore s'ils sont transcendants ou non incluent :
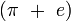 ,
, 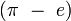 ,
, 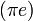 ,
,  ,
, 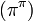 ,
, 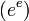 ,
, 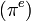
- La constante d'Euler-Mascheroni
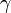 (dont on ignore même si elle est irrationnelle)
(dont on ignore même si elle est irrationnelle)
- La constante de Catalan (dont on ignore aussi si elle est irrationnelle)
- La constante d'Apéry
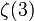 (dont on sait qu'elle est irrationnelle)
(dont on sait qu'elle est irrationnelle)
Tous les nombres de Liouville sont transcendants, néanmoins les nombres transcendants ne sont pas tous des nombres de Liouville. Tout nombre de Liouville doit avoir des termes non bornés dans son développement en fraction continue, donc en utilisant un argument de dénombrement, on peut montrer qu'il existe des nombres transcendants qui ne sont pas des nombres de Liouville. En utilisant le développement explicite en fraction continue de e, on peut montrer que e n'est pas un nombre de Liouville. Kurt Mahler montra en 1953 que
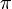 n'est pas non plus un nombre de Liouville. Il a été conjecturé que toutes les fractions continues à termes bornés qui ne sont pas périodiques à partir d'un certain rang sont transcendantes (les fractions continues périodiques à partir d'un certain rang correspondent aux irrationnels quadratiques).
n'est pas non plus un nombre de Liouville. Il a été conjecturé que toutes les fractions continues à termes bornés qui ne sont pas périodiques à partir d'un certain rang sont transcendantes (les fractions continues périodiques à partir d'un certain rang correspondent aux irrationnels quadratiques).Esquisse de démonstration de la transcendance de e
La première démonstration que e est transcendant date de 1873. Nous suivrons maintenant la stratégie de David Hilbert (1862 - 1943) qui donna une simplification de la démonstration originale de Charles Hermite. L'idée est la suivante :
Supposons, dans le but de trouver une contradiction, que e est algébrique. Alors, il existe un ensemble fini de coefficients entiers
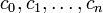 satisfaisant l'équation :
satisfaisant l'équation :et c0 et cn sont tous deux différents de zéro.
Dépendant de la valeur de n, nous précisons un entier positif suffisamment grand k (pour nos besoin ultérieurs) et multiplions les deux cotés de l'équation ci-dessus par
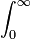 , où la notation
, où la notation 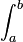 sera utilisé dans cette démonstration comme abréviation de l'intégrale :
sera utilisé dans cette démonstration comme abréviation de l'intégrale :![\int^{b}_{a}:=\int^{b}_{a}x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,dx\,](/pictures/frwiki/49/14711a42cf8b99b6fa55cab24141308e.png) .
.
Nous arrivons à l'équation :
qui peut maintenant être écrite sous la forme
où
Le plan d'attaque maintenant est de montrer que pour un k suffisamment grand, les relations ci-dessus sont impossible à satisfaire parce que
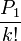 est un entier différent de zéro et
est un entier différent de zéro et 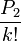 ne l'est pas.
ne l'est pas.
Le fait que
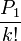 soit un entier différent de zéro résulte de la relation
soit un entier différent de zéro résulte de la relationqui est valide pour tout entier positif j et peut être prouvé par récurrence au moyen d'une intégration par parties.
Pour montrer que
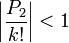 pour un k suffisamment grand
pour un k suffisamment grand
nous noterons d'abord que
![x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,](/pictures/frwiki/50/2ba7da49229818516d2f45b0de775a44.png) est le produit des fonctions
est le produit des fonctions ![[x(x-1)(x-2)\cdots(x-n)]^{k}\,](/pictures/frwiki/101/e4111e47104eb5fa732fb159a47ebe08.png) et
et  . En utilisant la borne supérieure pour
. En utilisant la borne supérieure pour 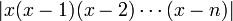 et
et 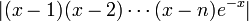 sur l'intervalle [0,n] et en employant le fait que
sur l'intervalle [0,n] et en employant le fait que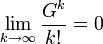 pour chaque nombre réel G
pour chaque nombre réel G
est alors suffisant pour achever la démonstration.
Une stratégie similaire, différente de l'approche originale de Lindemann, peut être utilisée pour montrer que le nombre
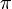 est transcendant. En outre, la fonction gamma, certaines estimations pour e et des faits à propos des polynômes symétriques jouent un rôle vital dans la démonstration.
est transcendant. En outre, la fonction gamma, certaines estimations pour e et des faits à propos des polynômes symétriques jouent un rôle vital dans la démonstration.Pour des informations détaillées concernant les démonstrations de transcendances de
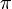 et
et  , voir les références et les liens externes.
, voir les références et les liens externes.Voir aussi
- théorie de la transcendance, l'étude des questions relatives aux nombres transcendants
Références
- (de) David Hilbert, « Über die Transcendenz der Zahlen e und π », Mathematische Annalen 43:216–219 (1893).
- (en) Alan Baker, Transcendental Number Theory, Cambridge University Press, 1975 (ISBN 0-521-39791-X).
Liens externes
- (fr) Article du 13 mai 1844 de Liouville sur les nombres transcendants (avec une analyse de M. Mendès-France, mathématicien) (site BibNum)
- (fr) Démonstration d'Hermite de la transcendance de e (1873), présentée et analysée sur le site BibNum.
- (en) Démonstration que e est transcendant
- [pdf] (de) Démonstration que e est transcendant
- [pdf] (de) Démonstration que π est transcendant
- [pdf] (fr) Démonstration de la transcendance de e et π
- [pdf] (fr) Démonstration de la transcendance de e et π
- Portail des mathématiques
Catégorie : Nombre transcendant
Wikimedia Foundation. 2010.