- Theoreme de l'element primitif
-
Théorème de l'élément primitif
En mathématiques, et plus spécifiquement en algèbre, le théorème de l'élément primitif est un des théorèmes de base de la théorie des extensions finies de corps.
Le théorème établit une équivalence, si l'extension est finie, entre la notion d'extension séparable, le nombre de morphismes de l'extension dans la clôture algébrique laissant invariant le corps de base et l'existence d'un élément séparable (appelé élément primitif) générant l'extension.
Ce théorème fait partie des deux piliers de la théorie de Galois dans le cas des extensions finies. Il établit une équivalence qui introduit la notion de séparabilité. Il est utilisé par exemple pour la démonstration du théorème fondamental de la théorie de Galois.
Sommaire
Un exemple explicite
Il est souvent facile de construire explicitement un élément primitif. Ainsi, prenons
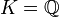 , et
, et 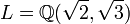 (L est une extension séparable de K, voir ci-dessous) ; montrons que
(L est une extension séparable de K, voir ci-dessous) ; montrons que 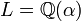 , avec
, avec 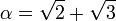 . Il est clair qu'il suffit de démontrer que
. Il est clair qu'il suffit de démontrer que 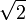 et
et  sont dans
sont dans 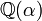 , or un calcul direct montre que
, or un calcul direct montre que 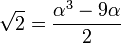 et que
et que 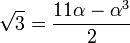 (en fait, la méthode proposée en note aboutit à
(en fait, la méthode proposée en note aboutit à  et à
et à 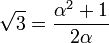 , et demande, pour retrouver les formules précédentes, de savoir calculer
, et demande, pour retrouver les formules précédentes, de savoir calculer 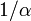 en fonction de
en fonction de  ).
).Motivation
Article détaillé: Extension séparable
Une démonstration purement calculatoire de l'existence d'un élément primitif dans le cas général (même en se restreignant aux nombres algébriques) est assez délicate[1], et il s'avère plus efficace de se placer dans le cadre plus vaste des extensions galoisiennes.
La théorie de Galois possède comme structure fondamentale le groupe de Galois, ce groupe permet de démontrer une série de résultats géométriques, comme la caractérisation des nombres constructibles pour déterminer par exemple les polygones réguliers constructibles à la règle et au compas, la résolution d'équations algébriques ou d'établir des résultats en théorie des nombres comme le grand théorème de Fermat dans beaucoup de cas particuliers.
Comme autre exemple de ce groupe, on peut citer la caractérisation des corps finis. Le groupe permet de déterminer la structure exacte du corps ainsi que la nature des différents polynômes à coefficients dans ce corps.
Pour permettre ces démonstrations, le groupe de Galois doit être suffisamment vaste, ce qui signifie deux propriétés : l'extension doit être séparable et normale. Un élément de l'extension est dit séparable si et seulement si son polynôme minimal à coefficients dans K ne possède pas de racines multiples dans sa clôture algébrique. Une extension est dite séparable si tous ses éléments le sont. Le théorème indique qu'il suffit qu'un élément bien choisi soit séparable pour que toute l'extension le soit. Cette propriété est importante car la racine d'un polynôme est toujours transformée par un élément du groupe de Galois en une autre racine. S'il existe des racines multiples, alors le groupe devient trop petit pour que le théorème fondamental de la théorie de Galois puisse s'appliquer.
Dans le cas où l'extension est de dimension finie en tant qu'espace vectoriel sur le corps de base K, si l'extension est séparable alors le nombre de morphismes de l'extension dans la clôture algébrique est le bon. Il existe de plus une propriété forte: il existe un élément l de l'extension tel que L est égal à K(l) c’est-à-dire que L est la plus petite extension contenant K et l et bien sûr l est séparable. On parle alors d'extension simple algébrique. La réciproque est aussi vraie et est constitutive du théorème de l'élément primitif.
Énoncé du théorème
Soit L une extension finie de dimension n sur un corps K, et Ω la clôture algébrique de K. Alors le théorème de l'élément primitif prend la forme suivante:
-
- Les quatre conditions suivantes sont équivalentes:
- L'extension L est séparable sur K.
- L'extension est engendrée par des éléments séparables.
- Il existe exactement n morphismes de L dans Ω laissant invariant K.
- L est une extension simple générée par un élément séparable (appelé élément primitif).
Remarque: Il existe d'autres expressions du théorème de l'élément primitif, par exemple: toute extension séparable finie est simple. Une autre forme est la suivante: l'extension L est simple si et seulement si elle contient un nombre fini d'extensions de K.
Cas des corps parfaits
La séparation est une propriété relativement fréquente dans les extensions algébriques. Par exemple si le corps K est de caractéristique 0 alors toute extension est séparable. La caractéristique d'un corps est nulle si l'addition réitérée de l'unité n'est jamais nulle, donc si son sous-corps premier est
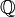 . En conséquence, toute extension du corps des nombres rationnels ou des nombres réels est séparable. Tout corps fini ne possède, lui aussi, que des extensions algébriques séparables.
. En conséquence, toute extension du corps des nombres rationnels ou des nombres réels est séparable. Tout corps fini ne possède, lui aussi, que des extensions algébriques séparables.Un corps qui n'admet que des extensions séparables est dit parfait.
Démonstration
- La proposition 1 implique la proposition 2
Le résultat est immédiat.
- La proposition 2 implique la proposition 3
C'est une conséquence des deux dernières propositions démontrées dans le paragraphe Morphisme dans la clôture algébrique.
- La proposition 3 implique la proposition 4
Supposons qu'il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3. Alors son polynôme minimal est de degré n, et K(l) est un espace vectoriel inclus dans L et de même dimension. Les deux espaces sont égaux et la proposition est démontrée. Il suffit alors de démontrer l'existence de l, ce qui est fait en fin de paragraphe.
- La proposition 4 implique la proposition 1
Soit l un générateur de L. l est d'ordre n et donc il existe n morphismes de L dans Ω laissant invariant K. Soit alors r un élément quelconque de L alors L est une extension de K(r) et chaque morphisme de L est la composée d'un morphisme de K(r) étendu à L et d'un morphisme de L laissant invariant K(r). Soit nr le nombre de morphismes de K(r) dans Ω laissant invariant K et n' le nombre de morphismes de L dans Ω laissant invariant K(r). Nous avons les relations :
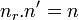 ,
, ![n_r\le[K(r):K]](/pictures/frwiki/99/cc20c7f2e9cfa3ea1deb074fae246421.png) ,
, ![n' \le[L:K(r)]](/pictures/frwiki/48/0fd79374c31964d8cc9cad11b9975295.png) et
et ![\displaystyle[L:K(r)].[K(r):K]=n](/pictures/frwiki/97/a62e9abec1b4810910e5b1ca44955281.png) . On en conclue que
. On en conclue que ![\displaystyle n_r=[L:K(r)]](/pictures/frwiki/56/8e0d8c9caf01cdbf3b11c6d8709338db.png) . Les images de r par les différents morphismes de K(r) dans Ω laissant invariant K sont distinctes deux à deux car sinon les morphismes seraient confondus. Le polynôme minimal de r admet donc [K(r):K] racines distinctes. Nous avons démontré que r est séparable.
. Les images de r par les différents morphismes de K(r) dans Ω laissant invariant K sont distinctes deux à deux car sinon les morphismes seraient confondus. Le polynôme minimal de r admet donc [K(r):K] racines distinctes. Nous avons démontré que r est séparable.- Si K est un corps fini, alors il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3.
Si K est un corps fini, alors le groupe multiplicatif associé à L est un groupe cyclique. Si l est choisi parmi les éléments générateurs du groupe, alors il possède n images distinctes par les n morphismes. Sinon, il existerait des morphismes confondus. Et la proposition est démontrée.
- Si K est un corps infini, alors il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3.
Considérons Vij l'ensemble des vecteurs de L ayant même image par le ie et le je morphisme. Vij est un sous-espace vectoriel différent de L. Une propriété des unions des espaces vectoriels montre que l'union des Vij n'est pas égal à L. Il existe donc un élément l de L qui n'est élément d'aucun Vij. Son polynôme minimal admet donc n racines distinctes. Ce polynôme minimal possède un degré qui divise n, d'après une propriété démontrée dans l'article Extension algébrique. Son degré est donc exactement n. l est donc générateur et séparable et la démonstration est terminée.
Note
- ↑ On en trouvera une esquisse, due à van der Waerden, dans le dernier lien externe proposé
Voir aussi
Liens externes
- (fr) Théorème de l'élément primitif à les mathématiques.net
- (en) Théorème de l'élément primitif à mathreference.com
- (en) Théorème de l'élément primitif à planetmath.org
- (en) Théorème de l'élément primitif sur le site de l'université de Cornell
Références
- R. et A. Douady Algèbre et théories galoisiennes Cedic/Fernand Nathan 1978
- S. Lang Algebre Dunod 2004
- P. Samuel Théorie algébrique des nombres Hermann Paris 1971
- Portail des mathématiques
Catégories : Théorie de Galois | Théorème d'algèbre -
Wikimedia Foundation. 2010.
