- Théorème d'Abel-Ruffini
-
Théorème d'Abel (algèbre)
 Pour les articles homonymes, voir Théorème d'Abel.
Pour les articles homonymes, voir Théorème d'Abel. Niels Henrik Abel (1802-1829) présente la première démonstration rigoureuse et complète du théorème qui porte maintenant son nom.
Niels Henrik Abel (1802-1829) présente la première démonstration rigoureuse et complète du théorème qui porte maintenant son nom.
En mathématiques, et plus précisément en algèbre le théorème d'Abel, parfois appelé théorème d'Abel-Ruffini ou encore théorème de Ruffini, indique qu'il existe des polynômes de degré supérieur ou égal à cinq et à coefficients complexes dont les racines ne s'expriment pas par radicaux.
Ce théorème est parfois mal interprété, il n'indique pas qu'une équation de degré cinq à coefficients complexes n'admet pas de racine. Le théorème de d'Alembert-Gauss indique même l'inverse, ce type de question admet toujours au moins une solution. En revanche, cette solution ne s'exprime pas toujours par radical, ce qui signifie qu'il n'est pas toujours possible d'exprimer cette racine à partir des coefficients du polynôme, de la valeur 1, des quatre opérations auxquelles on ajoute le radical, c'est-à-dire l'extraction des racines nièmes.
Ce résultat est exprimé pour la première fois par Paolo Ruffini, puis démontré rigoureusement par Niels Henrik Abel. La version que l'on présente parfois est celle d'Évariste Galois qui donne une condition nécessaire et suffisante d'expression des racines sous forme de radicaux.
Sommaire
Préambule
Signification du théorème
Le théorème d'Abel, avec le théorème de d'Alembert-Gauss, forment les deux théorèmes fondamentaux de la théorie des équations, c'est-à-dire la théorie qui traite des équations polynomiales ou équivalentes. Une équation est dite polynomiale si elle est de la forme P(X) = 0, où P désigne un polynôme. Le théorème de d'Alembert-Gauss indique qu'une équation à coefficients dans les entiers, les rationnels, les réels ou les complexes admet au moins une racine complexe.
Des méthodes numériques comme la méthode de Newton-Raphson ou celle de Laguerre s'appliquent indépendamment du degré de l'équation. Si n, le degré du polynôme, est petit, il existe aussi des méthodes dites algébriques pour résoudre l'équation. Ainsi, si n est égal à 2, et si P s'écrit ax2 + bx + c, les racines sont données par la célèbre formule
 , où b2 − 4ac est le discriminant du polynôme ; on dit que
, où b2 − 4ac est le discriminant du polynôme ; on dit que 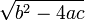 est un radical. Des formules analogues (mais beaucoup plus compliquées) existent pour les polynômes de degré 3 ou 4, comme le montre les méthodes de Cardan et de Ferrari.
est un radical. Des formules analogues (mais beaucoup plus compliquées) existent pour les polynômes de degré 3 ou 4, comme le montre les méthodes de Cardan et de Ferrari.L'expression suivante d'un cosinus est aussi une expression par radical. Elle est obtenue à partir du polynôme cyclotomique correspondant aux racines dix-septièmes de l'unité (on pourrait aussi utiliser le polynôme de Tchebychev T17), et permet la construction à la règle et au compas de l'heptadécagone régulier (le polygone réguler à 17 côtés) qui fut découverte par Gauss (c'est le théorème de Gauss-Wantzel) :
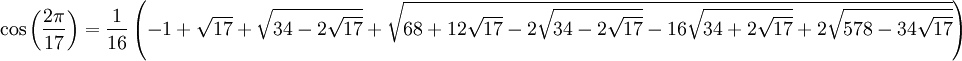
Mais malgré l'exemple précédent, pour les degrés strictement supérieurs à 4, et en dépit de plusieurs siècles d'efforts, aucune formule générale analogue à celles des degrés 2, 3 et 4 n'avait pu être trouvée. Le théorème d'Abel exprime le fait qu'aucune formule de cette nature n'existe. Une méthode pour exprimer néanmoins les racines consiste à faire usage d'une famille de fonctions plus vaste que celle des racines nièmes, telle que celle des fonctions elliptiques ; mais les formules ainsi obtenues n'ont qu'un intérêt théorique ; en pratique, il est bien plus intéressant d'obtenir des valeurs approchées à l'aide, par exemple, de la méthode de Newton.
Expressions du théorème
L'expression la plus proche de celle d'Abel[1] est la suivante :
-
- Il n'existe pas de formule générale exprimant les solutions de l'équation du cinquième degré sous forme de radicaux.[2]
Évariste Galois est l'auteur d'une forme plus aboutie du théorème. Sa méthode est celle généralement utilisée pour démontrer le théorème. Cette formulation prend parfois le nom de Théorème d'Abel[3], souvent aucun nom n'est indiqué[4] et plus rarement le nom de théorème d'Abel-Galois[5]. Sa formulation est plus générale car elle s'applique à un corps commutatif K quelconque et non plus uniquement au corps C des nombres complexes. Elle indique aussi si une équation algébrique est résoluble par radicaux ou non.
Soit P un polynôme à coefficients dans un corps commutatif K et L son corps de décomposition. Si l'extension L est séparable alors :
-
- Le polynôme P est résoluble par radicaux si et seulement son groupe de Galois est résoluble.
Le polynôme X5 - 3X - 1 n'est pas résoluble par radicaux, c'est-à-dire qu'il n'est pas possible d'exprimer les racines de ce polynôme sous forme de radical. Le groupe de Galois de ce polynôme est le groupe symétrique d'ordre 5, qui n'est pas résoluble (une démonstration est en donnée dans l'article groupe alterné).
Radical
Soit K un corps commutatif et L une extension de K.
-
- On appelle radical de K dans L un élément l de L tel qu'il existe une puissance de l élément de K. De même, on appelle radical d'une suite S d'éléments de L, un élément de l de L tel qu'il existe une puissance de l, élément de la suite S.
- On dit qu'un élément l de L s'exprime par radicaux de K si et seulement s'il existe p suites finies Si avec i variant de 0 à p-1 telles que:
- - S0 est une suite de K
- - Si i est un entier compris entre 1 et p - 1 alors Si est une suite de combinaisons linéaires à coefficients dans K de radicaux de la suite Si-1.
- - l est une combinaison linéaire à coefficients dans K d'éléments de la suite Sp-1
- On dit qu'un polynôme est résoluble ou résoluble par radicaux si et seulement si toutes ses racines s'expriment par radicaux de K.
Formalisme de la théorie de Galois
L'expression de la version de Galois du théorème fait usage d'un vocabulaire particulier, issu de la théorie de Galois. Le corps de décomposition L de P désigne le plus petit corps contenant K ainsi que toutes les racines de P. On montre qu'un tel corps existe et est unique, à un isomorphisme près. On suppose que L est une extension séparable, c'est-à-dire qu'aucun polynôme irréductible à coefficient dans L ne possède de racine multiple. Cette propriété de séparabilité est très générale, elle est toujours vérifiée si le corps K est de caractéristique nulle, comme pour Q, R ou C ou encore n'importe quel corps de nombres.
Une structure clé pour exprimer cette version du théorème est le groupe de Galois, c'est le groupe des automorphismes de corps de L, laissant invariant K. Ce groupe est non vide puisqu'il contient au moins l'identité. On démontre que si n est la dimension de L, vu comme espace vectoriel sur K, le groupe de Galois est fini et d'ordre n (cf l'article extension de Galois).
Comprendre le théorème suppose la compréhension du terme groupe résoluble. Pour que le théorème d'Abel s'applique, il faut que le groupe de Galois G de P soit au moins un peu commutatif. Un premier cas de figure est celui ou G est commutatif au sens classique du terme, le groupe est résoluble. Il peut aussi exister un sous-groupe normal G1 de G commutatif et un groupe H abélien tel que le produit semi-direct de G1 par H soit isomorphe à G. Dans ce cas, le théorème d'Abel s'applique encore et H est isomorphe au groupe quotient G/G1. Dans le cas général :
-
- Un groupe G est dit résoluble lorsqu'il existe une suite finie G0, G1,...,Gn de n+1 sous-groupes de G telle que :
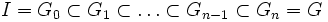
-
- où Gk, pour tout k compris entre 0 et n; est un sous-groupe distingué de Gk+1 et le groupe quotient Gk+1/Gk est abélien. Le groupe I désigne le sous-groupe constitué uniquement de l'élément neutre de G.
Histoire
Une vision d'ensemble de la théorie des équations, traitant en particulier du théorème d'Abel, est donnée dans l'article théorie des équations.
Genèse
Si la première étude systématique des équations algébriques remonte au VIIIe siècle, dans l'Abrégé du calcul par la restauration et la comparaison du mathématicien arabe Al-Khawarizmi[6], l'idée d'associer une structure de groupe à l'équation n'apparaît qu'au XVIIIe siècle. Joseph-Louis Lagrange (1736 1813) met en évidence la relation entre les propriétés d'un groupe de permutations des racines et la possibilité de résolution d'une équation cubique ou quartique[7]. S'il est possible de voir dans ces travaux l'origine de l'utilisation des permutations dans ce domaine, en revanche, ne sont utilisés ni la loi de composition ni l'ensemble des permutations comme une structure propre. Son approche est toutefois suffisante pour émettre un sérieux doute sur l'existence d'une formule exprimant les racines d'un polynôme quelconque de degré n, si n est strictement supérieur à 4.
Paolo Ruffini
Paolo Ruffini (1765 1822) est le premier à affirmer que l'équation générale et particulièrement l'équation quintique n'admet pas de solution. Il reprend la démarche de Lagrange qui montre que toutes les méthodes utilisées jusqu'ici reviennent à des cas particuliers d'une approche plus générale. Ruffini montre que la méthode de Lagrange ne peut fournir, pour l'équation de degré cinq, de formule équivalente à celle de Cardan pour le degré trois. Il publie un livre sur cette question[8] en 1799.
La communauté scientifique de l'époque ne reconnaît pas son travail. Il envoie son livre à Lagrange en 1801, mais n'obtient aucune réponse. Une présentation officielle à l'Académie des sciences, n'obtient pas plus de succès. Lagrange, Legendre (1752 1833) et Lacroix, trois mathématiciens sont chargés d'évaluer la validité de sa preuve. Le rapport décrit son travail comme sans importance, sa démonstration comporte une lacune, rien n'indique qu'il n'existerait pas d'autres méthodes, différentes de celle de Lagrange et donc de toutes celles trouvées jusque là, et qui permettrait une résolution par radical. Une nouvelle tentative, auprès de la Royal Society anglaise obtient une réponse plus sympathique: si un tel travail n'entre pas dans sa compétence, les résultats ne semblent néanmoins pas contenir d'erreur. Deux autres publications en 1803 et 1808 n'auront guère plus de succès. Pour les mathématiciens de l'époque, le résultat est soit faux, soit anecdotique. Seul Augustin Louis Cauchy (1789 1857) comprend la profondeur de son travail. Il lui envoie une lettre en 1821 dans laquelle il indique à la fois la validité et l'importance de la question traitée. Cauchy généralise[9] le résultat sur les permutations à la base des travaux de Ruffini.[10]
Niels Henrik Abel
Après une tentative infructueuse en 1821, le mathématicien norvégien Niels Henrik Abel (1802 1829) publie, à ses propres frais un petit texte de six pages[11]. A la différence des travaux de Ruffini, ce document représente une preuve complète du théorème. Il obtient néanmoins une incompréhension analogue à celle des textes précédents. Même Carl Friedrich Gauss (1777 1855) juge le sujet sans intérêt. La lettre d'Abel sera retrouvée après la mort de Gauss non décachetée. En 1801, ce mathématicien avait exprimé dans sa thèse que la recherche de solution par radicaux était sans intérêt, il suffisait de donner un nom quelconque à la racine. Il est vrai qu'en terme de technique numérique, il est beaucoup plus simple d'utiliser une méthode comme celle de Newton pour obtenir une valeur approchée d'une racine, la résolution par radical ne possède plus au XIXe siècle le même intérêt qu'il avait les siècles précédents pour le calcul numérique. Et, si ce n'est pas pour obtenir une approximation numérique, alors autant utiliser une lettre pour décrire la racine. Même Cauchy, qui reçoit Abel en 1826 daigne à peine jeter un coup d'œil à ses travaux.
D'autres articles furent écrits entre 1826 et 1828, contenant la preuve de l'impossibilité de la résolution dans le cas général. Les travaux d'Abel finissent par convaincre la communauté scientifique. En 1830 Cauchy retrouve son manuscrit, et Abel finit par obtenir le grand prix de mathématiques de l'Académie des sciences la même année à titre posthume.[12]
Évariste Galois
Après les travaux d'Abel, seuls trois éléments manquent pour une expression finale du théorème: une approche effective, la condition nécessaire et suffisante de résolubilité de l'équation et une compréhension profonde des mécanismes qui rendent possible la résolubilité. C'est Évariste Galois (1811 1832) qui réalise ces trois progrès.
Son approche subit la même incompréhension que ses prédécesseurs. Ses premiers écrits, présentés à l'Académie des sciences dès 1829 sont définitivement perdus. Un article[13] de l'auteur écrit en 1831 est redécouvert par Joseph Liouville (1809 1882) qui le présente à la communauté scientifique en 1843 en ces termes: "...J'espère intéresser l'Académie en lui annonçant que dans les papiers d'Évariste Galois j'ai trouvé une solution aussi exacte que profonde de ce beau problème : Étant donnée une équation irréductible, décider si elle est ou non résoluble par radicaux.". L'apport de Galois est majeur, G. Verriest[14] le décrit dans les termes suivants:"le trait de génie de Galois c'est d'avoir découvert que le nœud du problème réside non pas dans la recherche directe des grandeurs à adjoindre, mais dans l'étude de la nature du groupe de l'équation. Ce groupe (...) exprime le degré d'indiscernabilité des racines (...). Ce n'est donc plus le degré d'une équation qui mesure la difficulté de la résoudre mais c'est la nature de son groupe."
Exemples
Le cas du second degré
Considérons le cas où le polynôme P[X] est de degré deux à coefficients rationnels n'ayant pas de racine rationnelle. Quitte à diviser l'équation, il est possible de considérer que :
![P[X]=X^2-pX+q\,](/pictures/frwiki/56/815108508fa54221b328e8a28456de6a.png)
Notons x1 et x2 les deux racines de l'équation. On en déduit :
![P[X]=X^2-pX+q=(X-x_1)(X-x_2)\quad donc\quad x_1+x_2=p \; et\; x_1.x_2=q\;](/pictures/frwiki/53/5e3be1ec12555f5701a77e28e2abafad.png)
L'extension est de degré deux et L est un espace vectoriel sur les rationnels de dimension deux. Comme l'extension est galoisienne le groupe de Galois G est d'ordre deux, il existe donc un morphisme m du groupe de Galois différent de l'identité tel que m² soit égal à Id l'identité de L. Le polynôme minimal de m est donc un diviseur de X²-1. Les valeurs propres de m sont donc 1 car l'ensemble des rationnels est invariant par m et -1 car m est différent de l'identité. Considérons alors une base de L (1,r) telle que r soit une valeur propre de m et telle que x1 = a + r. Alors x2 s'exprime aussi dans la base, il existe donc deux rationnels a' et b' tels que x2 = a' + b'r.
Or la somme des racines est rationnelle donc b' est égal à -1. De plus, le produit des racines est aussi rationnel donc a' est égal à a. On en déduit :
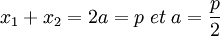
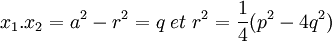
Le groupe de Galois permet donc une résolution effective de l'équation quadratique.
Le cas du degré trois
Généralités
Considérons le cas où le polynôme P[X] est de degré trois à coefficients rationnels et irréductible. Quitte à diviser l'équation et à translater la variable, il est possible de considérer que:
![P[X]=X^3+pX-q\;](/pictures/frwiki/56/8f175e9d9c89036ef85cc24c856c155d.png)
Notons x1, x2 et x3 les trois racines de l'équation. On en déduit:
![P[X]=X^2-pX+q=(X-x_1)(X-x_2)(X-x_3)\;](/pictures/frwiki/53/5999ce9924ca34340ef981ea31edf44d.png)
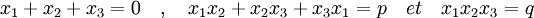
Le corps de décomposition L contient la racine x1 dont le polynôme minimal est de degré trois. Et L est au moins de dimension trois. Le groupe de Galois de P[X] est isomorphe à un sous-groupe de S3 le groupe symétrique d'ordre trois et est donc inclus dans un groupe d'ordre six. Le groupe de Galois est au moins d'ordre trois car L est au moins de dimension trois sur le corps des rationnels. Il est au plus d'ordre six. Le groupe de Galois est donc soit isomorphe à S3 soit à A3 le groupe alterné d'ordre trois isomorphe au groupe cyclique d'ordre trois.
A3 est un groupe résoluble car il est abélien, S3 contient un sous-groupe distingué A3 et A3 ainsi que S3/A3 sont abéliens car ils contiennent respectivement trois et deux éléments. En conséquence S3 est aussi résoluble. Dans tous les cas, le groupe de Galois est résoluble, donc le théorème d'Abel-Ruffini garantit que le polynôme l'est aussi.
Détermination du groupe de Galois
Le groupe de Galois est égal à S3 si et seulement s'il contient un élément dont la signature (le groupe de Galois est ici identifié au groupe des permutations des racines) est égal à -1. Soit g un élément du groupe ; on a alors l'égalité:
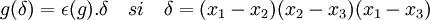
où ε(g) désigne la signature de g. On en déduit que le groupe de Galois contient un élément de signature impaire si et seulement si δ a pour image par un élément du groupe − δ. Dans le cas contraire δ est invariant par tous les éléments du groupe, ce qui est une condition nécessaire est suffisante pour que δ soit un rationnel (cf la quatrième propriété du paragraphe sur le théorème fondamental de la théorie de Galois. On remarque de plus que le carré de ce nombre est toujours un rationnel. On vérifie alors que:
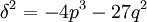
On en déduit la condition nécessaire et suffisante:
-
- Le groupe de Galois de P[X] est égal à A3 si et seulement si - 4p3 - 27q2 est un carré dans l'ensemble des rationnels.
Calcul des racines
Dans l'extension Q[δ], le groupe de Galois ne contient que des éléments d'ordre trois. Pour plus de commodité, considérons alors l'extension L1 comme égale à Q[δ, j] où j désigne la première racine cubique de l'unité (celle de partie imaginaire strictement positive). Les deux éléments δ et j sont des éléments d'ordre deux, L1 ne peut donc contenir les racines du polynôme. Soit m le morphisme du groupe de Galois défini par:
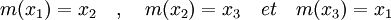
Le morphisme m est défini par une permutation de signature paire, et le groupe de Galois contient les trois permutations de signature paire, m est donc bien un élément du groupe.
Le polynôme caractéristique de m considéré comme un endomorphisme de l'espace vectoriel L sur L1 est égal à X³-1 = 0. Il admet trois racines 1, j et j² qui sont donc trois valeurs propres. Il existe donc une base de vecteurs propres et x1 = u + v + w où u (respectivement v), (respectivement w) est soit un vecteur propre de valeur propre j (respectivement j²) (respectivement 1) soit le vecteur nul. Il ne reste alors plus qu'à calculer u, v et w en fonction des coefficients du polynôme.
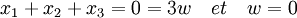
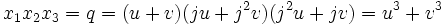
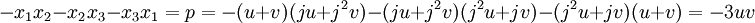
Le système d'équations suivant permet alors de conclure:

Un exemple de degré seize
Article détaillé : polynôme cyclotomique.Certains polynômes, malgré leurs degrés élevés, sont résolubles par radicaux. Carl Friedrich Gauss (1777 1855) a étudié les polynômes cyclotomiques en 1801[15] pour, entre autres choses, construire à la règle et au compas l'heptadécagone, c’est-à-dire le polygone régulier à 17 cotés. Il a considéré le polynôme suivant:
![P[X]=\sum_{i=0}^{16} X^i](/pictures/frwiki/55/7345adfea9d0c039cadc4d055b034363.png)
C'est le polynôme cyclotomique correspondant au troisième nombre premier de Fermat. Montrons que son groupe de Galois est isomorphe au groupe cyclique d'ordre seize.
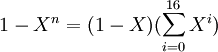
L'égalité précédente montre que les seize racines d'ordre dix-sept différentes de l'unité sont des racines du polynôme. Soit z la première racine primitive: exp(i.2.pi/17) et m un morphisme de l'extension du corps des nombres rationnels contenant les seize racines différentes de un. Alors m(z) est aussi une racine, il existe donc un entier p tel que m(z)= zp. On en déduit que si n est un entier alors : m(zn)= zn.p. Réciproquement si p est un entier compris entre un et seize alors l'application qui à zn associe zn.p définit bien un élément du groupe de Galois. Le groupe de Galois est donc un groupe à seize éléments isomorphe au groupe cyclique d'ordre seize.
La fin des calculs se trouve dans le paragraphe Cas de l'heptadécagone.
Un contre-exemple de degré cinq
Article détaillé : Groupe alterné.L'article détaillé montre que l'équation X5 - 3X - 1 = 0 ne possède pas de racine s'exprimant par radicaux dans l'ensemble Q des nombres rationnels.
Démonstration
Si le groupe est résoluble, alors le polynôme l'est.
On suppose dans ce paragraphe que L est une extension séparable, et donc L est une extension de Galois (cf l'article corps de décomposition).
Un corps de décomposition est un espace vectoriel de dimension finie sur le corps de base, soit n cette dimension.
Comme le montre la méthode de Cardan, l'adjonction des n racines de l'unité, même si elle n'est pas toujours nécessaire, est bien utile. On suppose donc que K contient les n racines de l'unité, c’est-à-dire les n racines du polynôme Xn - 1.
La démonstration du caractère résoluble du polynôme est souvent réalisée en deux temps:
-
- Si G est abélien alors il existe une base de L considérée comme un espace vectoriel de K de radicaux de K.
Remarque 1: souvent le corps initial est celui des nombres rationnels, et K est l'extension cyclotomique d'ordre n.
Remarque 2: s'il existe une base de radicaux, alors tout élément de L et en particulier les racines du polynôme s'exprime comme combinaison linéaire de radicaux, l'équation polynomiale est donc résoluble par radicaux.
-
- Si G est un groupe résoluble Alors tout élément de L possède une expression par radicaux sur K.
Démonstrations-
- Si G est abélien alors il existe une base de L considérée comme un espace vectoriel sur K de radicaux de K.
L'extension L est un corps de décomposition séparable. L'article sur les corps de décomposition démontre que L est une extension de Galois finie. En conséquence G contient exactement n éléments, et un élément laissé invariant par chaque élément de G appartient nécessairement à K (cf deuxième proposition du paragraphe sur les propriétés élémentaires.
Le groupe de Galois est aussi une représentation de groupe dans l'espace vectoriel L, chaque élément du groupe m étant maintenant considéré comme un automorphisme d'espace vectoriel. Dans le cas de la représentation d'un groupe fini abélien dans un espace vectoriel de dimension finie, alors il existe une base qui diagonalise chaque automorphisme du groupe (cf Diagonalisation de la représentation d'un groupe fini commutatif. Chaque valeur propre est racine de l'équation X n - 1 = 0, d'après le théorème de Lagrange. Une valeur propre est donc une racine n-ième de l'unité.
Soit (r1, ..., rn) une base qui diagonalise tous les éléments de G, et (λ1, ..., λn) les valeurs propres associées à m un élément quelconque de G alors:
![\forall i \in [1,n] \quad m(r_i^n)=m(r_i)^n=\lambda_i^n.r_i^n=r_i^n \,](/pictures/frwiki/100/d2cf5541cda8588341c5fe3b70405d5b.png)
Or L est une extension de Galois, en conséquence, rin, laissé invariant par chacun des automorphismes du groupe, est un élément de K. Ce qui démontre que la base choisie est une base de radicaux. La proposition est donc démontrée.
-
- Si G est un groupe résoluble, alors tout élément de L possède une expression par radicaux sur K.
Dire que G est résoluble signifie qu'il existe une suite finie
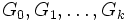 de k + 1 sous-groupes de G telle que :
de k + 1 sous-groupes de G telle que :
Où, si i est compris entre 0 et k - 1 Gi est un sous-groupe distingué de Gi + 1 et le groupe quotient Gi + 1 / Gi est abélien. Ici, I désigne le groupe réduit à l'élément neutre. Démontrons alors la proposition par récurrence sur k.
- Si k est égal à 1, alors le groupe de Galois de L est abélien. En conséquence il existe une base L formée par des radicaux de K. Toute racine s'exprime dans cette base, ce qui démontre la proposition.
- Supposons la propriété vraie à l'ordre p et supposons que k est égal à p + 1.
Considérons alors le corps Lk-1 choisi comme étant égal aux élements de L laissé invariant par tous les automorphismes de G1. Alors le théorème fondamental de la théorie de Galois assure que Lk-1 est une extension de Galois dont le groupe de Galois est isomorphe à G / G1. Cette extension vérifie donc l'hypothèse de récurrence et tous ses éléments s'expriment par radicaux sur K.
Le théorème fondamental assure aussi que L est une extension de Galois sur Lk-1 ayant comme groupe de Galois le groupe abélien G1. Donc tout élément de L s'exprime par radicaux sur Lk-1 et donc sur K. Et la proposition est démontrée.
Si un polynôme est résoluble, alors son groupe de Galois l'est.
La démonstration de la réciproque se réalise en trois temps. Dans un premier temps, l'objectif est de décrire l'extension L sous une forme plus maniable que le fait que les racines du polynôme aient une expression par radicaux. Comme précédemment, on suppose que K contient le groupe des racines n-ièmes de l'unité où n est le ppcm de tous les ordres des racines.
-
- Si toutes les racines de P[X] s'expriment par radicaux, alors il existe une suite d'extensions:
![K=F_0\subset F_1\subset \ldots\subset F_{k-1}\subset F_k = F \mbox { avec } \forall i \in [1,k] \; \exists \alpha_i \in F_i \mbox { tel que } \alpha_i^{p_i} \in F_{i-1} \mbox { et } F_i=F_{i-1}(\alpha_i)](/pictures/frwiki/50/2541bf19a920a98663f56fd917a99379.png)
- où pi est une suite de nombres premiers et F une extension contenant L.
La suite de la démonstration consiste à analyser une des extensions de la suite:
-
- Si Fi est un corps contenant une racine primitive p-ième de l'unité où p est un nombre premier, si α est un élément de Ω tel que αp est élément de Fi, alors Fi(α) de F est une extension de Galois abélienne.
Les deux propositions précédentes permettent alors de conclure:
-
- Si P[X] est résoluble, alors son groupe de Galois l'est.
Démonstrations-
- Existence de la suite d'extensions (Li).
On remarque, dans une premier temps que tout radical s'écrit comme composé de radicaux dont l'ordre est un nombre premier, car:
![\forall p,q \in \mathbb{N}^* \quad \sqrt[pq]{x}=\sqrt[p]{\sqrt[q]{x}} \;](/pictures/frwiki/52/4b2f0010f3416c3607c69973f2c24571.png)
Soit R l'ensemble des radicaux d'ordre un nombre premier utilisés dans les définitions des différentes racines de P[X]. R est un ensemble fini, notons k son cardinal. Notons F l'extension du corps K engendrée par R. Montrons alors par récurrence sur k l'existence de la suite d'extensions.
- cas où k est égal à 1.
R ne contient qu'un seul élément α1 et la suite définie par F0 = K et F1 = K(α1) = F vérifie la proposition.
- Supposons la propriété démontrée à l'ordre m et supposons que k soit égal à m + 1.
Comme R est l'ensemble des radicaux d'ordre un nombre premier utilisé dans l'expression des racines, il contient au moins un élément α1 qui est un radical de K. Soit F1 = K(α1), F est une extension de F1 engendrée par m éléments. Il existe par hypothèse de récurrence une suite:
![F_1\subset F_2\subset \ldots\subset F_{k-1}\subset F_k = F \mbox { avec } \forall i \in [2,k] \; \exists \alpha_i \in F_i \mbox { tel que } \alpha_i^{p_i} \in F_{i-1} \mbox { et } F_i=F_{i-1}(\alpha_i)](/pictures/frwiki/54/6a13cf01ddf9e6bf7de1f5640666111a.png)
L'adjonction de K à cette suite démontre la proposition.
-
- Si Fi est un corps contenant une racine primitive p-ième de l'unité où p est un nombre premier, si α est un élément de Ω tel que αp est élément de Fi, alors Fi(α) est une extension abélienne.
- Montrons que F(α) est une extension séparable.
Notons r une racine primitive p-ième de l'unité. Si α est un élément de F alors la proposition est évidente. Dans le cas contraire, Xp - αp est un polynôme annulateur de α. Ce polynôme est séparable car ses racines sont de la forme rk. α ou k est un entier compris entre 1 et p, et elles sont toutes distinctes. Le polynôme minimal de α est un diviseur du polynôme précédent, il est donc séparable. En conclusion le théorème de l'élément primitif montre que l'extension F(α) est séparable.
- Montrons que F(α) est une extension normale.
F(α) est engendré par la famille 1,α, ..., αp-1 elle est donc de dimension inférieure ou égale à p. Tout morphisme m de F(α) dans la clôture algébrique de K est défini exactement par sa valeur en α. Cette valeur est une racine du polynôme Xp - αp et il existe donc k tel que m(α) = rk α. Réciproquement toute valeur entière k comprise entre 0 et p - 1 définit un morphisme. Tous ses p morphismes distincts laissent F(α) stable. Ce qui montre que F(α) est une extension normale.
- Montrons que F(α) est une extension abélienne.
L'extension est normale et séparable, elle est donc galoisienne. Il suffit de remarquer que le groupe de Galois a pour ordre un nombre premier pour conclure que ce groupe est cyclique, donc abélien.
-
- Si P[X] est résoluble, alors son groupe de Galois l'est.
Montrons par récurrence sur k que Fi est une extension galoisienne de K.
- Si k est égal à 1, alors F est égal à K(α) et la proposition précédente démontre que F est une extension galoisienne de groupe un groupe abélien donc résoluble.
- Supposons la propriété vraie pour m et supposons de k = m + 1.
Alors Fk-1 est une extension galoisienne de K, F est une extension galoisienne de Fk-1 d'après le résultat précédent. On en déduit que F est une extension galoisienne de K. Soit Gi où i est un entier compris entre 0 et k le sous-groupe du groupe G de Galois de F laissant invariant Fi. Comme Fi est une extension galoisienne de K, Gi est un sous-groupe distingué de G et donc de Gi+1 si i est plus petit que k. La démonstration précédente montre que le groupe de Galois de l'extension Fi+1 de Fi est abélien, le quotient de Gi+1 par Gi isomorphe à ce groupe est donc aussi abélien. G est donc résoluble.
L'extension L de K est incluse dans F et est de Galois car c'est un corps de décomposition inclus dans une extension séparable. Le groupe H laissant invariant L est donc un sous-groupe distingué de F. G est résoluble, H est un sous-groupe distingué de G, donc G/H est résoluble (cf groupe résoluble). Or G/H est le groupe de Galois de L (cf théorème fondamental de la théorie de Galois). La proposition est ainsi démontrée.
Voir aussi
Notes
- ↑ N. Abel Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré Journal de Crelle 1826
- ↑ Voir D. Müller Résolution d'équations Apprendre-en-ligne.net
- ↑ Y. Laszlo Théorie de Galois Ecole Polytechnique
- ↑ Adrien Douady et Régine Douady, Algèbre et théories galoisiennes [détail des éditions] p 320
- ↑ J. Brillet Factorisation d'un polynôme Laboratoire d'astrophysique de Bordeaux
- ↑ Amy Dahan-Dalmedico, Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986 (ISBN 2020092380)[détail des éditions]
- ↑ Joseph-Louis Lagrange Réflexions sur la résolution algébrique des équations Nouveaux mémoires de l'académie royale des sciences et belles lettres de Berlin (1771) Lire sur Gallica
- ↑ Paolo Ruffini Théorie générale des équation, où il est montré que la résolution de l'équation algébrique générale de degré supérieur à quatre est impossible 1799
- ↑ A. L. Cauchy Sur le nombre des valeurs qu'une fonction peut acquérir lorsqu'on permute de toutes les manières possibles les quantités qu'elle renferme Journal de l'Ecole Polytechnique 1815
- ↑ L'essentiel des informations de ce paragraphe provient de : J. J. O'Connor E. F. Robertson Paolo Ruffini Site historique de l'Université de St Andrew
- ↑ Niels Henrik Abel Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré 1824
- ↑ L'essentiel de ces informations proviennent du site J. J. O'Connor E. F. Robertson Niels Henrik Abel Site historique de l'Université de St Andrew
- ↑ Evariste Galois sur les conditions de résolubilité des équations algébriques 1846 Journal de Liouville
- ↑ G. Verriest Œuvres Mathématiques d'Évariste Galois 1951 Gauthier-Villars, Paris
- ↑ Carl Friedrich Gauss Disquisitiones arithmeticae 1801
Liens externes
- (fr) Démonstration du Théorème d'Abel-Ruffini par Serge Hubleau
- (en) Références historiques de l'université de St Andrews
- (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
- (fr) Groupe de Galois dans les-mathématiques.net
- (fr) Une approche naïve du groupe de Galois
Références
- R. et A. Douady Algèbre et théories galoisiennes Cedic/Fernand Nathan 1978
- S. Lang Algebre Dunod 2004
- P. Samuel Théorie algébrique des nombres Hermann Paris 1971
- Portail des mathématiques
Catégories : Équation polynomiale | Théorie de Galois | Théorème de mathématiques | Théorème d'algèbre -
Wikimedia Foundation. 2010.