- Compactification de Stone–Čech
-
En mathématiques, et plus précisément en topologie générale, la compactification de Stone–Čech (découverte en 1937 par Marshall Stone (en)[1] et Eduard Čech[2]) est une technique de construction d'un espace compact prolongeant un espace topologique donné X ; plus précisément, il s'agit de la construction d'une application universelle allant de X vers un espace compact βX.
Sommaire
Définition
Le compactifié de Stone–Čech, βX, d'un espace topologique X est le plus grand compact « engendré » par X. Plus rigoureusement :
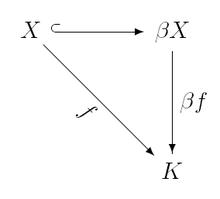
Définition — Soit X un espace topologique. Le compactifié de Stone–Čech de X, noté βX, est un espace compact Y, avec une application i de X vers Y, tel que pour tout espace compact Z et toute application continue f de X vers Z, il existe une application continue unique g de Y vers Z telle que

On verra dans les sections suivantes que le couple (i,Y) est essentiellement unique (à unique isomorphisme près), et que l'axiome du choix permet de démontrer son existence pour tout espace topologique X. En revanche, X ne peut être considéré comme un sous-espace (dense) de βX (autrement dit i n'est un plongement) que si X est un espace de Tychonov ; i peut même ne pas être injective, elle le sera si et seulement si X est un espace d'Urysohn.
Propriété universelle et fonctorialité
La définition précédente est un exemple de propriété universelle : elle affirme qu'il existe un morphisme βf unique rendant le diagramme ci-contre commutatif. Autrement dit, X → βX est initial parmi les compacts K munis d'un morphisme X → K. Comme toute propriété universelle, ceci caractérise βX à homéomorphisme près[3] et cet homéomorphisme est unique.
Certains auteurs demandent de plus que X soit un espace de Tychonov, ou même un espace localement compact, pour les raisons suivantes :
- L'application allant de X vers son image dans βX est un homéomorphisme si et seulement si X est un espace de Tychonov.
- Cette application est un homéomorphisme vers un sous-espace ouvert de βX si et seulement si X est localement compact.
La construction de Stone–Čech peut être effectuée pour des espaces X quelconques, mais l'application X → βX n'est alors pas un homéomorphisme, et peut même ne pas être injective.
La propriété d'extension des applications fait de β un foncteur allant de Top (la catégorie des espaces topologiques) vers Comp (la catégorie des espaces compacts). Si nous notons U le foncteur d'inclusion (qui est un foncteur d'oubli) de Comp vers Top, les applications de βX vers K (pour K dans Comp) correspondent bijectivement aux applications de X vers UK (en considérant leur restriction à X et en utilisant la propriété universelle de βX). Autrement dit, Hom(βX,K) = Hom(X,UK), ce qui veut dire que β est adjoint à gauche de U. Ceci entraîne que Comp est une sous-catégorie réflexive (en) de Top, avec β comme réflecteur.
Constructions
La section précédente a montré l'unicité (à homéomorphisme près) du compactifié de Stone–Čech. Les constructions équivalentes suivantes nécessitent toutes l'axiome de choix ; seules les deux premières s'appliquent à des espaces X généraux.
À l'aide de produits
Une tentative de construction du compactifié de Stone–Čech de X est de prendre l'adhérence de l'image de X dans
 , où le produit est pris sur l'ensemble de toutes les applications continues de X vers des espaces compacts C. Cette construction, sous cette forme, échoue, parce que cette collection d'applications est une classe propre et non un ensemble ; il est cependant possible de la rendre correcte, par exemple en restreignant les compacts C à l'ensemble des couples (Y,T), où Y=P(P(X)) (l'ensemble des parties de l'ensemble des parties de X), et où T est une des topologies rendant Y compact. Y est choisi suffisamment grand pour que son cardinal majore celui de tout compact C pour lequel il existe une application continue de X dans C d'image dense.
, où le produit est pris sur l'ensemble de toutes les applications continues de X vers des espaces compacts C. Cette construction, sous cette forme, échoue, parce que cette collection d'applications est une classe propre et non un ensemble ; il est cependant possible de la rendre correcte, par exemple en restreignant les compacts C à l'ensemble des couples (Y,T), où Y=P(P(X)) (l'ensemble des parties de l'ensemble des parties de X), et où T est une des topologies rendant Y compact. Y est choisi suffisamment grand pour que son cardinal majore celui de tout compact C pour lequel il existe une application continue de X dans C d'image dense.En utilisant l'intervalle unité
Considérons l'application F de X vers [0,1]C, définie par
où C est l'ensemble de toutes les applications continues de X vers [0,1]. On voit que F est continue, si l'on munit [0,1]C de la topologie produit. D'après le théorème de Tychonov, on sait que [0,1]C est compact puisque [0,1] l'est, donc l'adhérence de F(X) dans [0,1]C est une compactification de X.
Pour montrer qu'on obtient bien le compactifié de Stone–Čech, il faut contrôler la propriété universelle. On le vérifie d'abord pour K = [0,1], où l'extension cherchée de f : X → [0,1] est la projection sur la "f-ème" coordonnée dans [0,1]C. pour généraliser cela à un compact K quelconque, on remarque que K peut (comme tout espace complètement régulier) être plongé dans un cube (un produit de la forme [0,1]I), on étend comme précédemment chacune des fonctions coordonnées, et on prend le produit de ces extensions.
Cette construction réussit parce que l'intervalle unité est un cogénérateur de la catégorie des espaces compacts : cela veut dire que si f et g sont deux applications (continues) distinctes entre deux compacts A et B, il existe une application h de B vers [0,1] telle que hf et hg sont distinctes. Tout autre cogénérateur pourrait être utilisé pour la même construction.
À l'aide d'ultrafiltres
Si X est discret, on peut construire βX comme l'ensemble de tous les ultrafiltres sur X, muni de la topologie dite topologie de Stone[4]. X est identifié au sous-ensemble de βX formé des ultrafiltres triviaux.
Pour vérifier la propriété universelle dans ce cas, on remarque que pour f : X → K avec K compact et F un ultrafiltre sur X, on a un ultrafiltre f(F) sur K, qui converge vers un élément (unique) x, puisque K est compact ; on définit alors βf(F) = x, qui est une extension continue de f pour la topologie de Stone.
Cette construction est un cas particulier de celle de l'espace de Stone (en) d'une algèbre de Boole, appliquée ici à l'algèbre de l'ensemble des parties de X. Elle peut être généralisée à des espaces de Tychonov arbitraires en utilisant des filtres maximaux d'ensembles de zéros de fonctions continues de X vers R, ou simplement des filtres maximaux de fermés si l'espace est normal.
En utilisant des C*-algèbres
Dans le cas où X est un espace de Tychonov, le compactifié de Stone-Čech peut être identifié avec le spectre (en) de la C*-algèbre Cb(X) des fonctions continues bornées sur X, munie de la norme sup.
Le cas des entiers naturels
La compactification de Stone–Čech des entiers naturels
Dans le cas où X est localement compact, par exemple
 (pour la topologie discrète) ou
(pour la topologie discrète) ou  , c'est un sous-espace ouvert de βX et d'ailleurs de toute compactification (cette condition est également nécessaire, car tout ouvert d'un compact est localement compact). Dans ce cas, on s'intéresse souvent à l'espace complémentaire
, c'est un sous-espace ouvert de βX et d'ailleurs de toute compactification (cette condition est également nécessaire, car tout ouvert d'un compact est localement compact). Dans ce cas, on s'intéresse souvent à l'espace complémentaire  . Cet ensemble est un fermé de βX, et donc un compact. Pour
. Cet ensemble est un fermé de βX, et donc un compact. Pour  muni de la topologie discrète, on note
muni de la topologie discrète, on note  (mais cette notation n'est pas utilisée dans le cas d'un X général).
(mais cette notation n'est pas utilisée dans le cas d'un X général).On peut voir
 comme l'ensemble des ultrafiltres sur
comme l'ensemble des ultrafiltres sur  , muni de la topologie engendrée par les ensembles de la forme
, muni de la topologie engendrée par les ensembles de la forme  pour
pour  .
.  correspond à l'ensemble des ultrafiltres triviaux, et
correspond à l'ensemble des ultrafiltres triviaux, et  à l'ensemble des ultrafiltres libres ; cette construction a été décrite (et généralisée à des espaces de Tychonov quelconques) dans la section #À l'aide d'ultrafiltres ci-dessus.
à l'ensemble des ultrafiltres libres ; cette construction a été décrite (et généralisée à des espaces de Tychonov quelconques) dans la section #À l'aide d'ultrafiltres ci-dessus.L'étude de
 , en particulier de
, en particulier de  , est un domaine important de la topologie générale moderne. Les résultats principaux motivant cette étude sont les théorèmes de Parovicenko qui, pour l'essentiel, caractérisent
, est un domaine important de la topologie générale moderne. Les résultats principaux motivant cette étude sont les théorèmes de Parovicenko qui, pour l'essentiel, caractérisent  si l'on admet l'hypothèse du continu ; il s'agit des théorèmes suivants :
si l'on admet l'hypothèse du continu ; il s'agit des théorèmes suivants :- Tout compact admettant une base formée d'au plus
 ouverts (voir aleph) est image de
ouverts (voir aleph) est image de  par une fonction continue (ce résultat n'utilise pas l'hypothèse du continu, mais est moins intéressant en son absence).
par une fonction continue (ce résultat n'utilise pas l'hypothèse du continu, mais est moins intéressant en son absence).
- En admettant l'hypothèse du continu,
 est (à isomorphisme près) le seul espace de Parovicenko (en).
est (à isomorphisme près) le seul espace de Parovicenko (en).
Ces résultats furent d'abord démontrés en considérant des algèbres de Boole et en utilisant la dualité de Stone (en).
Application : l'espace dual de l'espace des suites réelles bornées
Le compactifié βN peut être utilisée pour caractériser ℓ∞(ℕ) (l'espace de Banach formé des suites bornées à valeurs réelles ou complexes, muni de la norme sup), ainsi que son dual topologique.
Étant donnée une suite bornée
 , il existe une boule fermée B (du corps des scalaires R ou C) qui contient l'image de a ; a est donc une application de
, il existe une boule fermée B (du corps des scalaires R ou C) qui contient l'image de a ; a est donc une application de  vers B. Comme
vers B. Comme  est discret, a est continue. Comme B est compacte, il existe donc (d'après la propriété universelle) une extension unique
est discret, a est continue. Comme B est compacte, il existe donc (d'après la propriété universelle) une extension unique  , qui ne dépend pas du choix de B.
, qui ne dépend pas du choix de B.Cette extension est donc une application de l'espace des suites (de scalaires) bornées vers l'espace des fonctions continues allant de
 vers les scalaires,
vers les scalaires, .
.
Cette application est surjective, puisque toute application de
 est bornée, et peut donc être restreinte à une suite bornée. Elle est de plus injective, car si nous munissons les deux espaces de la norme sup, c'est même une isométrie ; en effet, en prenant dans la construction précédente la plus petite boule B possible, on voit que la norme de la suite étendue ne peut grandir (l'image de cette fonction, bien que pouvant contenir des scalaires qui ne font pas partie de la suite, reste incluse dans la boule).
est bornée, et peut donc être restreinte à une suite bornée. Elle est de plus injective, car si nous munissons les deux espaces de la norme sup, c'est même une isométrie ; en effet, en prenant dans la construction précédente la plus petite boule B possible, on voit que la norme de la suite étendue ne peut grandir (l'image de cette fonction, bien que pouvant contenir des scalaires qui ne font pas partie de la suite, reste incluse dans la boule).Ainsi,
 peut être identifié avec
peut être identifié avec  . Ceci nous permet d'utiliser le théorème de représentation de Riesz, qui montre que le dual topologique de
. Ceci nous permet d'utiliser le théorème de représentation de Riesz, qui montre que le dual topologique de  peut être identifié à l'espace des mesures de Borel finies sur
peut être identifié à l'espace des mesures de Borel finies sur  .
.Enfin, il faut remarquer que cette technique se généralise à l'espace
 d'un espace mesurable arbitraire X. Cependant, au lieu de simplement considérer l'espace βX des ultrafiltres sur X, la construction appropriée utilise l'espace de Stone (en) Y de l'algèbre des mesures sur X : les espaces C(Y) et
d'un espace mesurable arbitraire X. Cependant, au lieu de simplement considérer l'espace βX des ultrafiltres sur X, la construction appropriée utilise l'espace de Stone (en) Y de l'algèbre des mesures sur X : les espaces C(Y) et  sont isomorphes en tant que C*-algèbres tant que X vérifie la condition (toujours satisfaite en pratique) que tout ensemble de mesure positive contienne un sous-ensemble de mesure positive finie.
sont isomorphes en tant que C*-algèbres tant que X vérifie la condition (toujours satisfaite en pratique) que tout ensemble de mesure positive contienne un sous-ensemble de mesure positive finie.L'addition dans le compactifié de Stone–Čech des entiers
Les entiers (positifs) forment un monoïde pour l'addition. Il se trouve que cette opération peut être prolongée (mais non de manière unique) à
 , transformant cet espace également en monoïde, quoique, de manière assez surprenante, en un monoïde non commutatif.
, transformant cet espace également en monoïde, quoique, de manière assez surprenante, en un monoïde non commutatif.Pour tout sous-ensemble
 et tout
et tout  , posons
, posonsÉtant donnés deux ultrafiltres F et G sur
 , on définit leur somme par
, on définit leur somme parcet ensemble est encore un ultrafiltre, et l'opération + est associative (mais non commutative) sur
 et prolonge l'addition de
et prolonge l'addition de  ; 0 (ou plus exactement l'ultrafiltre trivial contenant{0}) étant élément neutre pour + sur
; 0 (ou plus exactement l'ultrafiltre trivial contenant{0}) étant élément neutre pour + sur  . Cette addition est également continue à droite, au sens où pour tout ultrafiltre F, l'application de
. Cette addition est également continue à droite, au sens où pour tout ultrafiltre F, l'application de  vers
vers  définie par
définie par  est continue.
est continue.Notes et références
- (en) Marshall Stone, « Applications of the theory of Boolean rings to general topology », dans Trans. Amer. Math. Soc., vol. 41, 1937, p. 375–481 [lien DOI]
- (en) Eduard Čech, « On bicompact spaces », dans Annals of Mathematics, vol. 38, 1937, p. 823–844 [lien DOI]
- En effet, si i : X → Y et j : X → Z, deux applications continues de X dans des espaces compacts Y et Z, ont cette propriété, alors le morphisme βj : Y → Z et le morphisme βi : Z → Y sont inverses l'un de l'autre.
- On en trouvera une description détaillée dans (en) Russell C. Walker, The Stone-Čech compactification, Springer, 1974 (ISBN 9783540066996), p. 13
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stone–Čech compactification » (voir la liste des auteurs)
Voir aussi
Article connexe
Lien externe
(en) Dror Bar-Natan (en), « Ultrafilters, Compactness, and the Stone–Čech compactification », université de Toronto
Catégories :- Compacité
- Construction classique
Wikimedia Foundation. 2010.