Plan affine arguésien

Axiome de Desargues

Dans une approche axiomatique de la géométrie, un plan affine arguésien (ou desarguésien, ou de Desargues) est un plan affine vérifiant, en plus des axiomes d'incidence, l'axiome de Desargues :

Pour toutes droites d₁, d₂ et d₃ concourantes ou deux à deux parallèles, et pour tous points A₁ et B₁ incidents à d₁ ; A₂ et B₂ incidents à d₂ ; A₃ et B₃ incidents à d₃, si deux des trois couples de droites (A₁A₂) et (B₁B₂) ; (A₂A₃) et (B₂B₃) ; (A₁A₃) et (B₁B₃) sont des couples de droites parallèles, alors le troisième l'est aussi.

Cet axiome permet de définir homothéties et de translations. Ajouté aux axiomes d'incidence, il permet d'axiomatiser la structure de plan affine. Plus précisément, tout plan de Desargues se réalise comme un plan affine sur un corps K (non nécessairement commutatif), dont l'espace vectoriel directeur est défini comme l'ensemble des translations du plan ; le groupe multiplicatif de K s'identifie au groupe des homothéties de centre un point donné O. Réciproquement, tout plan affine, défini comme sous-espace affine de dimension 2 sur un corps K, satisfait les axiomes d'incidence et l'axiome de Desargues.

En dimension supérieure ou égale à 3, la propriété de Desargues est un théorème qui se démontre à l'aide des seuls axiomes d'incidence de la géométrie affine. Par conséquent un espace affine défini axiomatiquement à l'aide des seuls axiomes d'incidence est un espace affine tel que défini à partir des espaces vectoriels et un plan affine défini par les seuls axiomes d'incidence se plonge dans un espace affine de dimension supérieure si et seulement si l'axiome de Desargues est statisfait.

Pour un plan affine arguésien, la commutativité du corps sous-jacent équivaut à la la propriété de Pappus, que l'on peut prendre pour axiome. On appelle alors plan affine de Pappus un plan affine arguésien vérifiant l'axiome de Pappus. Il s'avère que l'axiome de Desargues devient alors redondant, d'après le théorème de Hessenberg.

Définition d'une homothétie-translation (dans un plan affine incident)

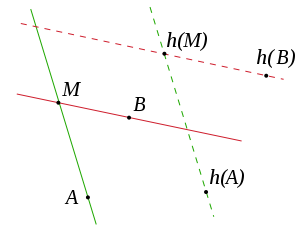
Une homothétie-translation est par définition une bijection h de l'ensemble des points d'un plan affine incident P telle que les deux conditions suivantes sont satisfaites :

• La transformation h préserve l'alignement des points. Autrement dit, h envoie trois points alignés sur trois points alignés. En particulier, h envoie tout point incident à une droite d sur des points incidents à une même droite, notée h(d). L'application h induit alors une bijection de l'ensemble des droites de P sur lui-même.
• La transformation h envoie toute droite sur une droite qui lui est parallèle.

L'identité est la seule homothétie-translation à fixer deux points distincts.

Considérons une bijection h de l'ensemble des points de P préservant l'alignement et envoyant toute droite sur une droite qui lui est parallèle. Supposons que h fixe deux points distincts, O et A.

Pour tout point M non incident à la droite (OA), la transformation h envoie la droite (OM) sur une droite contenant h(O) = O qui lui est parallèle. Par les axiomes d'incidence, cette droite est donc confondue à (OM) ; donc h(M) est incident à la droite (OM). De même, il est incident à la droite (AM). Par suite, h(M) est le point d'intersection des droites (OM) et (AM) ; il est donc confondu au point M. On a montré que h fixe tous les points non incidents à (OA).

Si N est un point incident à (OA), les axiomes d'incidence impliquent l'existence d'un point B non incident à (OA). Par ce qui précède, la transformation h fixe B, et par hypothèse, elle fixe O. Le même raisonnement que ci-dessus appliqués aux trois points non alignés O, B et N prouve que h fixe N.

De fait, la transformation h fixe tous les points de P, c'est l'identité.

 

Si la transformation h diffère de l'identité :

• Ou bien h ne fixe aucun point du plan P, auquel cas h est appelée translation ;
• Ou bien h fixe un unique point O, auquel cas h est appelée homothétie de centre O.

L'identité est considérée à la fois comme une translation et une homothétie. Le centre d'une homothétie non triviale (ie une homothétie différente de l'identité) est uniquement défini.

La définition d'une homothétie-translation ne s'appuie que sur les axiomes d'incidence.

Détermination d'une homothétie-translation (dans un plan affine de Desargues)

Construction de l'image d'un point par une homothétie-translation

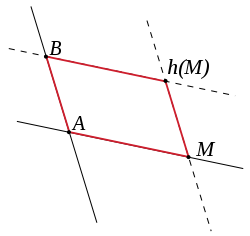
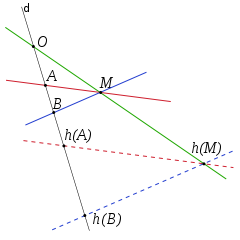
Dans un plan affine incident P, une homothétie-translation h est uniquement déterminée par les images h(A) et h(B) de deux points distincts A et B. Plus précisément, comme h envoie toute droite sur une droite qui lui est parallèle, l'image d'un point M non incident à la droite (AB) se définit uniquement comme le point d'intersection de la parallèle à (AM) passant par h(A) et de la parallêle à (BM) passant par h(B). L'image d'un point incident à (AB) se détermine par une construction analogue à partir de l'image de A et d'un point non incident à (AB) dont l'existence est assurée par les axiomes d'incidence.

Pour quatre points A, B, A' et B', l'existence d'une homothétie-translation envoyant A sur A' et B sur B' implique que les droites (AB) et (A'B') soient parallèles. Cependant, en l'absence de l'axiome de Desargues, même si cette condition nécessaire est validée, l'existence d'une telle homothétie-translation n'est pas assurée.

Dans un plan affine de Desargues, la donnée de quatre points A, B, A' et B' déterminent une unique homothétie-translation envoyant A sur A' et B sur B' si et seulement si les droites (AB) et (A'B') sont parallèles.

Définissons une bijection h de l'ensemble des points du plan affine de Desargues P :

• Les images h(A) et h(B) sont par définition les points A' et B'.
• L'image h(M) d'un point M non incident à la droite (AB) est défini comme le point d'intersection de la parallèle à (AM) passant par h(A) et de la parallèle à (BM) passant par h(B).
• Fixons un point C non incident à la droite (AB) dont l'existence est assurée par l'un des axiomes d'incidence. L'image h(N) d'un point N incident à la droite (AB) est défini comme le point d'intersection de la parallèle à (CN) passant par h(C) et de la droite (A'B').

.............

Détermination de la nature d'une homothétie-translation

La nature de la transformation peut être précisée dans le cas où les quatre points A, B, h(A) et h(B) sont non tous alignés. Cette hypothèse implique $h(A)\neq A$ et $h(B)\neq B$, et que les droites (Ah(A)) et (Bh(B)) sont non confondues. Selon leur position relative :

• Ou bien les droites (Ah(A)) et (Bh(B)) s'intersectent en un unique point O, et dans ce cas, h est une homothétie de centre O ;
• Ou bien les droites (Ah(A)) et (Bh(B)) sont parallèles, et dans ce cas, h est une translation.

Le résultat précédent peut être amélioré si on connait a priori la nature de l'homothétie-translation :

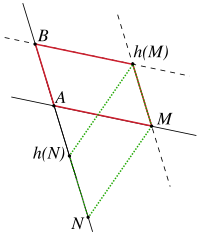
• Une translation non triviale du plan de Desargues est uniquement définie par l'image d'un point, donc par la donnée de deux points distincts. Si une translation envoie A sur B, alors elle envoie un point M non incident à (AB) sur le point d'intersection de la parallèle à (AB) passant par M et de la parallèle à (AM) passant par B. L'image d'un point N incident à (AB) se détermine par l'intermédiaire d'un point non incident à (AB). Les figures suivantes précisent la construction :

• Une homothétie non triviale du plan de Desargues est uniquement définie par son centre O et l'image h(A) d'un point A qui lui est distinct, donc par trois points distincts alignés. L'image d'un point M non incident à (OA) est définie comme le point d'intersection de la droite (OM) et de la parallèle à (AM) passant par h(A). L'image d'un point incident à la droite (OA) se définit par l'intermédiaire d'un point non incident. Les figurent suivantes précisent les constructions :

Composition

L'ensemble des homothéties-translations est stable par composition et l'inverse d'une homothétie-translation est une homothétie translation. En effet, si deux bijections de l'ensemble des points de P préservent l'alignement et envoie une droite sur une droite qui lui est parallèle, il en va de même de leurs composées. Cet ensemble forme donc un sous-groupe du groupe des bijections de l'ensemble des points de P, noté G :

L'ensemble des translations d'un plan affine de Desargues forme un sous-groupe de G, noté E(P) :

• L'inverse d'une translation est une translation. Un éventuel point fixe de l'inverse serait un point fixe de la translation T, ce qui est absurde si la translation est non triviale, par définition. Donc, l'inverse T ^{− 1} est une translation.
• La composée de deux translations est une translation. La composée $T'\circ T$ de deux translations T et T' est une homothétie-translation ; et pour établir que c'est une translation, il suffit par définition de prouver que l'existence d'un point fixe O de $T'\circ T$ implique que tout point est fixe. La translation T' envoie T(O) sur O. Il en va de même de la translation T ^{− 1}. Il s'en suit que T' = T ^{− 1} ou encore que $T'\circ T$ est l'identité.

Le groupe E(P) est commutatif ; sa loi est notée additivement.

Soient deux translations T et T' d'un plan affin de Desargues. Soit M un point quelconque de P. En nommant A = T'(M), les points A et T(A) déterminent uniquement l'image T(M) de M par la translation T. On suppose pour simplifier que les points M, A et T(A) sont non alignés. Le point T(M) est le point d'intersection de la parallèle à (AT(A)) passant par M et de la parallèle à (AM) passant par T(A).

De manière analogue, l'image T'(M) de M détermine uniquement l'image de T(M) par T' : le point $T'\circ T(M)$ est le point d'intersection de la parallèle à (MT(M)) passant par T'(M) et de la parallèle à (MT'(M)) passant par T(M). Ces parallèles sont respectivement $(T'(M),T\circ T'(M))$ et de $(T(M),T\circ T'(M))$. Ce point est donc $T\circ T'(M)$.

Par suite, il vient : $T'\circ T=T\circ T'$.

 

L'ensemble des homothéties de centre O forme un sous-groupe de G, noté K ^* (P,O) :

• L'inverse d'une homothétie de centre O est une homothétie-translation dont O est un point fixe ; donc une homothétie de centre O ;
• Pour les mêmes raisons, la composée de deux homothéties de même centre O est une homothétie de centre O.
• Le groupe des homothéties de centre 0 n'est pas en général commutatif. celle-ci dépend d'un axiome supplémentaire, la propriété de Pappus (version affine).

Structure d'espace affine

Espace affine de dimension 2

Article détaillé : Plan affine.

Un espace vectoriel (à gauche) sur un corps K (corps des scalaires) est un groupe commutatif (E, + ) muni d'une loi externe $K\times E\rightarrow E$, dont les éléments sont appelés vecteurs et vérifiant les relations de distributivité suivantes, valables pout tous vecteurs $v,w\in E$ et pour tous scalaires $\lambda,\nu\in K$ :

λ.(v + w) = λ.v + λ.w et λ.(ν.v) = (λν).v

Un espace affine d'espace vectoriel directeur E est un ensemble A muni d'une action libre et transitive du groupe commutatif (E, + ) sur A.

Les espaces affines de dimension 2 sont des plans affines de Desargues.

Réciproque

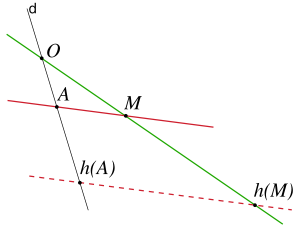
Réciproquement, tout plan affine de Desargues P est un espace affine dont l'espace vectoriel directeur (sur un corps non nécessairement commutatif) est le groupe des translations de P.

Si t est la translation envoyant O sur O', la conjugaison d'une homothétie de centre O' par la translation t est une homothétie de centre O. Par suite, la conjugaison par t induit un isomorphisme :

$\iota(t):K^*(P,O')\rightarrow K^*(P,O):h\mapsto t\circ h\circ t^{-1}$.

Ces isomorphismes se composent les uns les autres :

$\iota(t+t')=\iota(t)\circ \iota(t')= \iota(t')\circ \iota(t)$

Par ailleurs, la conjuguée d'une translation par une homothétie est une translation. Par suite, la conjugaison par une homothétie induit un isomorphisme (qui correspond à une homothétie vectorielle sur l'espace vectoriel des translations) :

$m(h):E(P)\rightarrow E(P):t\mapsto hth^{-1}$.

Pour toute translation t et pour toute homothétie h, on a :

m(ι(t)(h)) = m(h)

Le corps des scalaires est défini comme l'ensemble contenant un élément privilégié 0 et les classes d'homothéties définies à conjugaison près par une translation. Les lois sont uniquement définies de sorte que :

• 0 soit l'élément neutre de la loi d'addition et (la classe réduite à) l'identité, notée 1, est l'élément neutre pour la loi de multiplication ;
• Le produit des classes de deux homothéties de centre O est la classe de leur composition ;
• La somme des classes de deux homothéties de centre O envoyant un point A respectivement sur B et C est la classe de l'homothétie de centre O envoyant A sur l'image de B par la translation envoyant O sur C.

Vérifications des lois de distributivité

Volontairement, on ne fait pas de différence entre une homothétie et sa classe de conjugaison par des translations. Soient trois homothéties h, k et l de même centre O.

Par définition, (h + k) est l'unique homothétie envoyant A sur l'image de h(A) par l'unique translation T envoyant O sur k(A). Le produit l.(h + k) est l'unique homothétie de centre O envoyant A sur l[T(h(A))].

La transformation (lh + lk) est l'unique homothétie de centre O envoyant A sur l'image de lh(A) par l'unique translation T' envoyant O sur lk(A).

En nommant M = h(A) et N = k(A), la translation T'' = T' ^{− 1} est l'unique translation envoyant l(N) sur le centre O de l'homothétie l ; la translation T est (par définition) l'unique translation envoyant O sur N. Alors $T''\circ l\circ T$ est une homothétie de centre O et envoyant N sur l(N) :

$T''\circ l\circ T(O)=T''\left[l(N)\right]=O$.

Par suite, comme le centre O et l'image l(N) de N déterminent uniquement l'homothétie l, il vient :

$T''\circ l\circ T=l$ ou encore : $l\circ T=T'\circ l$.

En évaluant en h(A), il vient :

l[T(h(A))] = T'[lh(A)].

Les homothéties l(h + k) et lh + lk sont les uniques homothéties de centre O envoyant A respectivement sur l[T(h(A))] et T'[lh(A)]. Elles sont donc égales.

 

(Vérifications à faire, dessins, ...)

Axiome de Pappus affine : Si les points A₁, B₁ et C₁ sont alignés, de même que les points A₂, B₂ et C₂, et si les droites (B₁C₂) et (C₁B₂) sont parallèles, de même que les droites (A₁B₂) et (B₁C₂), alors les droites (A₁C₂) et (C₁A₂) sont parallèles.

Plan affine de Pappus

Un plan affine de Pappus est un plan affine arguésien vérifiant l'axiome de Pappus affine (énoncé ci-contre).

On suppose les points A₁, B₁ et C₁ alignés, les points A₂, B₂ et C₂ son également alignés sur une droite sécante avec la précédente en 0, et les droites (B₁C₂) et (C₁B₂) parallèles, de même que les droites (A₁B₂) et (B₁C₂).

Soit h₁, L'homothétie de centre 0 qui envoie A₁ sur B₁, et h₂, L'homothétie de centre 0 qui envoie C₂ sur B₂. On déduit des conditions de parallélisme que h₂ o h₁(A₁) = C₁ et h₁ o h₂(C₂)=A₂. Les droites (A₁B₂) et (B₁C₂) sont parallèles si et seulement si les deux homothéties de centre 0 (définies chacune par l'image d'un point distinct de O) h₂ o h₁ et h₁ o h₂ sont identiques, c'est-à-dire si et seulement si le produit des rapports des deux homothéties h₁ et h₂ est commutatif. Ceci assure l'équivalence (dans un plan affine arguésien) entre la commutativité du corps associé et l'axiome de Pappus, sachant que les cas particuliers de l'axiome non pris en compte sont soit triviaux (points A₁, B₁, C₁ et A₂, B₂, C₂ tous alignés), soit déjà démontrables dans un plan affine arguésien (droite passant par A₁, B₁ et C₁ parallèle à la droite passant par A₂, B₂, et C₂).

Voir aussi

• Plan_projectif arguésien

Bibliographie

• Emil Artin, Algèbre géométrique, Calmann-Lévy, traduction de Geometric algebra New York, Interscience Publishers, Inc., 1957, chap.II.
• Jacqueline Lelong-Ferrand, Fondements de la géométrie, PUF, 1985 (ISBN 2-13-038851-5) , chap. V.