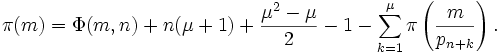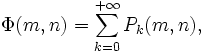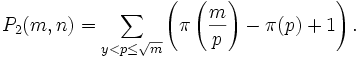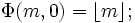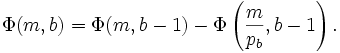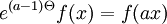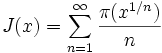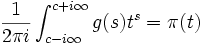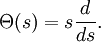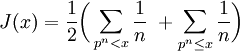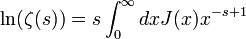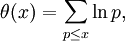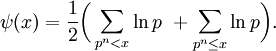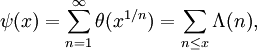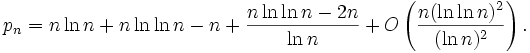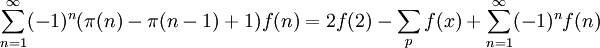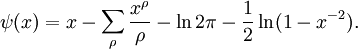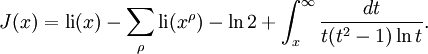- Fonction De Compte Des Nombres Premiers
-
Fonction de compte des nombres premiers
En mathématiques, la fonction de compte des nombres premiers est la fonction comptant le nombre de nombres premiers inférieurs ou égaux à un nombre réel x. Elle est notée
 (à ne pas confondre avec la constante π).
(à ne pas confondre avec la constante π).Sommaire
Historique
Depuis Euclide, il est connu qu'il existe des nombres premiers en quantité infinie. Pour affiner la connaissance de ces nombres, la théorie des nombres s'est attelée à en déterminer le taux de croissance. À la fin du XVIIIe siècle, Gauss[1] et Legendre[2] ont conjecturé que cette quantité était proche de
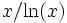 .
.De manière équivalente, on peut l'écrire

Cette affirmation constitue le théorème des nombres premiers, prouvé indépendamment par Hadamard et de La Vallée Poussin, en 1896, grâce à la fonction Zeta de Riemann. Une assertion équivalente est:
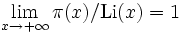 ,
,
où
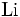 est la fonction Logarithme intégral.
est la fonction Logarithme intégral.Des estimateurs plus précis de
 sont aujourd'hui connus. Par exemple:
sont aujourd'hui connus. Par exemple: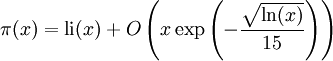 ,
,
Des preuves du théorème des nombres premiers n'utilisant pas l'analyse complexe furent proposée en 1948 par Atle Selberg et Paul Erdős.
Algorithmes d'évaluation de π(x)
Une façons simple de calculer
 , si
, si  est un nombre petit, est d'utiliser le crible d'Ératosthène de manière à trouver tous les premiers inférieurs à
est un nombre petit, est d'utiliser le crible d'Ératosthène de manière à trouver tous les premiers inférieurs à  et ensuite de les compter.
et ensuite de les compter.Une manière plus élaborée pour trouver
 a été inventée par Legendre: étant donné
a été inventée par Legendre: étant donné 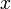 , si
, si  ,
, 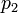 , …,
, …, 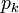 sont des nombres premiers distincts, alors le nombre d'entiers inférieurs ou égaux à x qui ne sont divisibles par aucun
sont des nombres premiers distincts, alors le nombre d'entiers inférieurs ou égaux à x qui ne sont divisibles par aucun 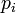 est
est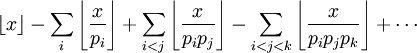 , (où
, (où  désigne la fonction Partie entière).
désigne la fonction Partie entière).
Ce nombre est donc égal à :
 où les nombres
où les nombres  ,
, 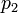 , …,
, …, 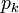 sont les nombres premiers inférieurs ou égaux à la racine carrée de
sont les nombres premiers inférieurs ou égaux à la racine carrée de 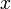 .
.Dans une série d'articles publiés entre 1870 et 1885, Ernst Meissel décrivit (et utilisa) une manière combinatoire pratique pour évaluer
 . Soit
. Soit  ,
, 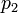 , …,
, …, 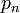 les premiers
les premiers 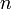 nombres premiers et notons par
nombres premiers et notons par 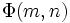 le nombre de nombres naturels inférieurs à
le nombre de nombres naturels inférieurs à 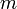 qui ne sont divisibles par aucun
qui ne sont divisibles par aucun 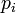 . Alors
. AlorsSoit un nombre naturel donné
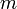 , si
, si ![n=\pi\left(\sqrt[3]{m}\right)\,](/pictures/frwiki/100/d1ff8835df047e0a61a9c57f3b6bb88e.png) et si
et si  , alors
, alorsEn utilisant cette approche, Meissel calcula
 , pour
, pour 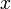 égal à 5x105, 106, 107, et 108.
égal à 5x105, 106, 107, et 108.En 1959, Derrick Lehmer étendit et simplifia la méthode de Meissel. Définissons, pour un réel m et pour des nombres naturels n, et k, Pk(m,n) comme le nombre de nombres inférieurs à m avec exactement k facteurs premiers, tous plus grands que pn. De plus, fixons
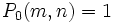 . Alors
. Alorsoù la somme actuelle possède seulement de manière finie plusieurs termes différents de zéro. Soit y désignant un entier tel que
![\sqrt[3]{m}\le y\le\sqrt{m}\,](/pictures/frwiki/57/9b72772fdd5ee03360226d6066b332ff.png) , et fixons
, et fixons 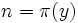 . Alors
. Alors 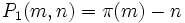 et
et 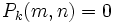 lorsque k ≥ 3. Par conséquent
lorsque k ≥ 3. Par conséquent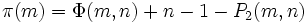 .
.
Le calcul de
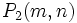 peut être obtenu de cette manière :
peut être obtenu de cette manière :D'un autre coté, le calcul de Φ(m,n) peut être fait en utilisant les règles suivantes :
En utilisant cette méthode et un IBM 701, Lehmer a été capable de calculer
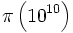 .
.Un mathématicien chinois Hwang Cheng, dans une conférence sur les fonctions de nombres premiers à l'université de Bordeaux utilisa les identités suivantes :[réf. nécessaire]
et en notant
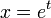 , en appliquant la transformée de Laplace aux deux cotés et en appliquant une somme géométrique sur
, en appliquant la transformée de Laplace aux deux cotés et en appliquant une somme géométrique sur 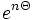 , on obtient l'expression :
, on obtient l'expression :Autres fonctions de compte des nombres premiers
D'autres fonctions de compte des nombres premiers sont aussi utilisées car elles sont plus pratiques pour travailler. Une d'elles est la fonction de compte des nombres premiers de Riemann, notée
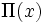 ou
ou 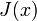 . Celle-ci possède des sauts de 1/n pour les puissances de nombres premiers pn, qui prennent une valeur à mi-chemin entre les deux cotés des discontinuités. Elle peut être aussi définie comme une transformation de Mellin inverse. Formellement, nous pouvons définir J par
. Celle-ci possède des sauts de 1/n pour les puissances de nombres premiers pn, qui prennent une valeur à mi-chemin entre les deux cotés des discontinuités. Elle peut être aussi définie comme une transformation de Mellin inverse. Formellement, nous pouvons définir J paroù p est un nombre premier.
Nous pouvons aussi écrire
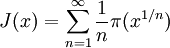 et
et
et en connaissant la relation entre la fonction log de la fonction Riemann et la fonction de von Mangoldt
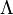 , et la formule de Perron, nous avons :
, et la formule de Perron, nous avons :excepté où se trouvent les discontinuités aux puissances de nombres premiers, et ainsi,
 peut être retrouvé à partir de J par l'inversion de Möbius.
peut être retrouvé à partir de J par l'inversion de Möbius.La fonction de Tchebychev pèse les nombres premiers ou les puissances de nombres premiers pn par ln p:
Excepté aux discontinuités des puissances de nombres premiers, nous avons
où
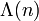 est la fonction de von Mangoldt.
est la fonction de von Mangoldt.Inégalités
Ci-dessous se trouvent quelques inégalités pour
 .
.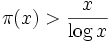 si x ≥ 17.
si x ≥ 17.
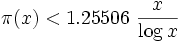 si x > 1.
si x > 1.
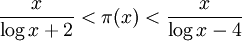 si x ≥ 55.
si x ≥ 55.
Les inégalites suivantes sont vérifiées par le nèmenombre premier, noté pn[3].
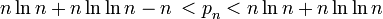 si n ≥ 6.
si n ≥ 6.
L'inégalité de gauche est vraie si n ≥ 1 et celle de droite si n ≥ 6 ; plus précisément encore, si n ≥ 40000, on a
Une approximation pour le ne nombre premier est
L'hypothèse de Riemann
L'Hypothèse de Riemann propose une estimation plus serrée de
 , équivalente à distribution plus régulière des nombres premiers:
, équivalente à distribution plus régulière des nombres premiers:Relation avec les sommes de nombres premiers
Si nous avons une somme de fonction sur tous les nombres premiers :
 et que nous souhaitons accélérer sa convergence, nous pouvons l'écrire sous la forme :
et que nous souhaitons accélérer sa convergence, nous pouvons l'écrire sous la forme :pour la série de gauche, nous avons pu appliquer la transformée d'Euler pour les séries alternées, en apportant que f(n)>f(n+1) et que les 2 séries convergent, elle relie aussi une série alternée avec sa somme de nombres premiers, d'autre part. La principale utilisation de ceci est que nous pouvons donner une bonne approximation en utilisant seulement quelques valeurs de la Fonction compte des nombres premiers.
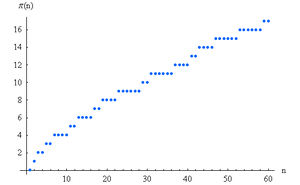
Table de π(x), x / ln x, et Li(x)
Voici une table qui montre le comportement comparé des trois fonctions π(x), x / ln x et Li(x) :
-
x π(x) π(x) − x / ln x Li(x) − π(x) x / π(x) 10 4 −0,3 2,2 2,500 102 25 3,3 5,1 4,000 103 168 23 10 5,952 104 1 229 143 17 8,137 105 9 592 906 38 10,425 106 78 498 6,116 130 12,740 107 664 579 44,158 339 15,047 108 5 761 455 332,774 754 17,357 109 50 847 534 2 592 592 1 701 19,667 1010 455 052 511 20 758 029 3 104 21,975 1011 4 118 054 813 169 923 159 11 588 24,283 1012 37 607 912 018 1 416 705 193 38 263 26,590 1013 346 065 536 839 11 992 858 452 108 971 28,896 1014 3 204 941 750 802 102 838 308 636 314 890 31,202 1015 29 844 570 422 669 891 604 962 452 1 052 619 33,507 1016 279 238 341 033 925 7 804 289 844 393 3 214 632 35,812 1017 2 623 557 157 654 233 68 883 734 693 281 7 956 589 38,116 1018 24 739 954 287 740 860 612 483 070 893 536 21 949 555 40,420 1019 234 057 667 276 344 607 5 481 624 169 369 960 99 877 775 42,725 1020 2 220 819 602 560 918 840 49 347 193 044 659 701 222 744 644 45,028 1021 21 127 269 486 018 731 928 446 579 871 578 168 707 597 394 254 47,332 1022 201 467 286 689 315 906 290 4 060 704 006 019 620 994 1 932 355 208 49,636 1023 1 925 320 391 606 818 006 727 37 083 513 766 592 669 113 7 236 148 412 51,939
La première colonne est la suite A006880 de l'Encyclopédie électronique des suites entières; la deuxième colonne est la suite A057835; et la troisième colonne, la suite A057752.
Formules pour les fonctions de compte des nombres premiers
Celles-ci sont de deux sortes, les formules arithmétiques et les formules analytiques. Ces dernières sont celles qui nous permettent de prouver le théorème des nombres premiers. Elles proviennent des travaux de Riemann et de von Mangoldt, et sont généralement connues comme formules explicites de fonctions L.
Nous avons l'expression suivante pour
 :
:Ici,
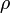 sont les zéros de la fonction zeta de Riemann dans la bande critique, où la partie réelle de
sont les zéros de la fonction zeta de Riemann dans la bande critique, où la partie réelle de 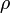 est comprise entre zéro et un. La formule est valide pour les valeurs de x plus grandes que un, qui est la région qui nous intéresse, et la somme des racines est convergente sous conditions, et devrait être prise en ordre croissant des valeurs absolues des parties imaginaires.
est comprise entre zéro et un. La formule est valide pour les valeurs de x plus grandes que un, qui est la région qui nous intéresse, et la somme des racines est convergente sous conditions, et devrait être prise en ordre croissant des valeurs absolues des parties imaginaires.Pour J, nous avons une formule plus compliquée :
De nouveau, la formule est valide pour x > 1, et
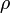 représente les zéros non triviaux de la fonction zeta ordonnés en accord avec leurs valeurs absolues. Le premier terme li(x) est le logarithme intégral habituel; néanmoins, il est moins facile de décrire ce que représente li dans les autres termes. La meilleure manière de concevoir cela est de considérer l'expression
représente les zéros non triviaux de la fonction zeta ordonnés en accord avec leurs valeurs absolues. Le premier terme li(x) est le logarithme intégral habituel; néanmoins, il est moins facile de décrire ce que représente li dans les autres termes. La meilleure manière de concevoir cela est de considérer l'expression 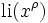 comme une abréviation de
comme une abréviation de 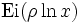 , où Ei est le prolongement analytique de la fonction intégrale exponentielle à partir des réels positifs vers le plan complexe muni d'une coupure le long des réels négatifs.
, où Ei est le prolongement analytique de la fonction intégrale exponentielle à partir des réels positifs vers le plan complexe muni d'une coupure le long des réels négatifs.Sources
- Jean-Paul Delahaye, Merveilleux nombres premiers, 2000, Éditions Belin. ISBN 2-84245-017-5
- Eric Bach and Jeffrey Shallit, Algorithmic Number Theory, volume 1, 1996, MIT Press. ISBN 0-262-02405-5, page 234, section 8.8.
- Garcia J.J An Approach to π(x) and Other Arithmetical Functions by Variational Principles General Science Journal [1]
- Leonard Eugene Dickson, History of the Theory of Numbers I: Divisibility and Primality, 2005, Dover Publications. ISBN 0-486-44232-2
Notes
- ↑ C'est en 1849, soit plus de 40 ans après la publication de Legendre, que Gauss indique, dans une correspondance avec Encke qu'il a conjecturé en 1793 que π(x) est approximativement égal à x / ln(x).
- ↑ A.M. Legendre, Essai sur la théorie des nombres, Seconde édition. Paris, Courcier (1808) p.394
- ↑ Pierre Dusart, « The kth prime is greater than k(ln k + ln ln k-1) for k>=2 », dans Mathematics of Computation, vol. 68, 1999, p. 411–415 [texte intégral]
- Portail des mathématiques
Catégories : Analyse réelle | Théorie analytique des nombres
Wikimedia Foundation. 2010.

![\Phi(m,n)=\Phi(m,n-1)-\Phi\left(\left[\frac{m}{p_n}\right],n-1\right),\,](/pictures/frwiki/55/74e174d3340797349db089ff76162460.png)