- Forme Bilinéaire
-
Forme bilinéaire
En mathématiques, le concept de forme bilinéaire est une notion algébrique s'appliquant à un espace vectoriel. Il correspond à une application qui, à deux vecteurs définis sur le même corps de nombres associe un scalaire. L'étude des formes bilinéaires entre dans la branche de l'algèbre linéaire.
Il existe une forme bilinéaire importante, le produit scalaire. Il définit une des distances les plus utilisées sur les espaces vectoriels de dimension finie ou infinie.
L'adjonction d'une distance à un espace vectoriel est suffisamment fréquente pour que cette structure s'applique à la quasi totalité des branches mathématiques. L'espace géométrique de notre univers étant doté d'une distance issue d'une forme bilinéaire, la physique utilise cette notion dans la quasi-totalité de ses théories, qu'elles soient classique, relativiste ou quantique.
Sommaire
Motivations
Les formes bilinéaires interviennent dans de nombreux domaines distincts des mathématiques. Elles forment une vaste classe d'outils utilisés pour résoudre des questions de nature très diverses.
Algèbre linéaire
Article détaillé : Algèbre linéaire.Le domaine natif des formes bilinéaires est celui de l'algèbre linéaire. Une forme bilinéaire est définie sur des espaces vectoriels et se généralisent sur les modules, structures de base de l'algèbre linéaire. Ces formes sont intimement liées aux applications linéaires. Le savoir associé à ces dernières permet d'éclairer la structure d'une forme bilinéaire et réciproquement les formes bilinéaires permettent d'élucider certaines particularité d'applications linéaires, par exemple dans le cas des endomorphismes autoadjoints.
Il existe un espace vectoriel particulier, jouant un grand rôle pour les formes bilinéaires : le dual. L'espace des formes bilinéaires est une copie exacte de celui des applications linéaires d'un espace dans un dual. La connaissance de la géométrie de l'espace ainsi que celle du dual permet d'élucider celle des applications linéaire de l'un vers l'autre et par la même occasion celle des formes bilinéaires. Dans le cas de la dimension finie, cette analyse est simple, le dual est une copie plus ou moins canonique de l'espace de départ.
Il existe une méthode générique pour construire des formes bilinéaires, le produit tensoriel fournissant un outil théorique pour démontrer certaines propriétés des formes bilinéaires. Il permet aussi de construire de nouveaux espaces vectoriels possédant une géométrie particulière dont les physiciens font grand usage. Ainsi le champ magnétique vérifie des propriétés de symétrie bien représentées par un espace particulier de formes bilinéaires. En plus de la structure d'espace vectoriel leur origine bilinéaire apporte des propriétés spécifiques, pour cette raison un nouveau terme est utilisé, celui de tenseur.
Géométrie
L'adjonction d'une forme bilinéaire bien choisie est source de formalisations de géométries. L'exemple le plus célèbre est peut-être celui des espaces euclidiens pour les espaces vectoriels sur le corps de nombres des réels dans le cas de la dimension finie. Cette forme bilinéaire appelée produit scalaire joue alors le même rôle que la forme bilinéaire canonique entre l'espace et son dual, permettant une formalisation plus concrète et plus facile d'accès.
Il n'est pas le seul exemple, un équivalent existe pour les nombres complexes. Un autre en dimension infinie existe avec les espaces préhilbertiens comportant un cas particulier essentiel, l'espace de Hilbert. En dimension finie, le choix d'une forme bilinéaire ayant d'autres propriétés permet de construire d'autres géométries. L'espace de Minkowski est construit à l'aide d'une approche de cette nature. Il offre un cadre géométrique à la théorie de la relativité restreinte.
L'influence des formes bilinéaires dans la géométrie ne se limite pas à la formalisation de nouveaux espaces. La relation entre certaines surfaces comme les quadriques et les formes bilinéaires est profonde. L'apport des différents outils provenant de l'algèbre linéaire permet une classification générale et pour une dimension quelconque.
Analyse fonctionnelle
Article détaillé : Analyse fonctionnelle (mathématiques).Il est fructueux de considérer un ensemble de fonctions issu de l'analyse, comme par exemple les fonctions du segment [0,1] à valeurs réelles et infiniment dérivable. Un ensemble de cette nature est un espace vectoriel de dimension infinie, les résultats de l'algèbre linéaire fondée sur l'utilisation de bases de cardinaux finis ne s'appliquent plus. L'étude de formes bilinéaires sur les espaces de cette nature s'avère féconde.
Un outil devient essentiel pour l'étude d'espaces vectoriels de cette nature, la topologie. Elle induit naturellement une autre topologie sur le dual. Il existe un cas particulier analogue à celui de la dimension finie, celui où le dual est une copie de l'espace des fonctions. Tel est le cas par exemple pour l'ensemble des fonctions de [0,1] à valeurs réelles qui sont de carrés intégrable. Un tel espace peut être muni d'un produit scalaire, apportant un service analogue à celui des espace euclidiens, il porte le nom d'espace de Hilbert.
Dans le cas général, le dual possède une structure différente de celle de l'espace de départ. Une autre forme bilinéaire est utilisée, celle qui à un élément du dual f et à un élément de l'espace x associe f(x). L'étude d'une telle structure est plus simple si la topologie est issue d'une norme possédant au moins une bonne propriété, la complétude. Un tel espace est appelé espace de Banach. La forme bilinéaire canonique entre le dual et l'espace prend souvent le nom de produit scalaire.
Arithmétique
La démarche des mathématiciens ayant étudié les espaces fonctionnels consiste à retirer une hypothèse auparavant toujours utilisée, celle de la dimension finie. Elle est finalement féconde et de nombreux théorèmes en analyse fonctionnelle tirent leur origine de l'étude d'une forme bilinéaire, comme un produit scalaire analogue à celui des espaces euclidiens ou issu de la forme canonique entre un espace et son dual. Une autre hypothèse peut être retirée, celle qui garantit que tout nombre différent de zéro du corps sous-jacent à l'espace vectoriel possède un inverse pour la multiplication.
Un exemple étudié depuis longtemps est celui des équations diophantiennes. Certaines d'entre elles s'écrivent comme la recherche des racines d'une équation polynomiale à plusieurs variables et à coefficients entiers. Les solutions recherchées sont celles qui s'expriment uniquement avec des nombres entiers. Un exemple célèbre et difficile est le grand théorème de Fermat. L'équation s'écrit xn + yn = zn. Les solutions peuvent être vues comme des points d'intersection entre Z3, où Z désigne l'ensemble des entiers, et une surface d'un espace géométrique de dimension trois. Un changement de repère permet parfois de simplifier l'expression d'une équation diophantienne. Pour être pertinent, ce changement de repère doit respecter la géométrie de l'espace. Il apparait comme une isométrie, c'est-à-dire une transformation respectant les distances et les angles, pour une bonne forme bilinéaire. Cette approche amène à l'étude des formes bilinéaires sur un module de dimension finie. « Module » signifie ici un quasi espace vectoriel, les scalaires ne sont simplement plus toujours inversibles. Ils peuvent, par exemple, se réduire à l'ensemble des entiers. Un exemple de cette nature est utilisé pour la démonstration du théorème des deux carrés de Fermat par Joseph-Louis Lagrange (1736-1813).
Définitions
Les formes bilinéaires s'appliquent dans un contexte vaste, en conséquence de multiples définitions sont associées à ce concepts. Ce paragraphe en décrit certaines, qui s'appliquent dans de nombreuses situations. Il en existe d'autres, développés dans les articles dédiés.
Définitions générales
Une forme désigne en mathématiques une application d'un espace vectoriel dans son corps de nombre (le corps de nombre désigne l'ensemble des nombres définissant la multiplication externe des vecteurs, en général ce sont les nombres réels ou complexes). Une forme bilinéaire est une application définie sur un couple de vecteurs x et y, son espace de départ est le produit cartésien de deux espaces vectoriels E et F ayant le même corps de nombres. Lorsque E et F désignent le même ensemble, on parle de forme bilinéaire sur E. (x|y) est une notation fréquente pour désigner l'image du couple (x,y) par la forme bilinéaire ; elle est utilisée dans le reste de l'article.
La forme est dite linéaire pour sa première variable si pour tout y0, l'application qui à x associe (x|y0) est linéaire. De même la forme est dite linéaire pour sa deuxième variable si pour tout x0, l'application qui à y associe (x0|y) est linéaire. Si les deux propriétés précédentes sont vérifiées, alors la forme est dite bilinéaire.
-
- Soit (.|.) une application de ExF dans K. La fonction (.|.) est dite bilinéaire si et seulement si elle est linéaire en ses deux variables.
Remarque: À toute forme bilinéaire sur un espace E est associée une forme quadratique. C'est l'application qui à un vecteur x associe le scalaire (x|x). Plus précisément, l'application qui, à chaque forme bilinéaire symétrique associe sa forme quadratique est un isomorphisme. L'isomorphisme réciproque associe à la forme quadratique χ la forme bilinéaire (.|.) définie par :
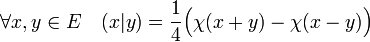
-
- La forme bilinéaire (.|.) définie par la ligne ci-dessus est dite forme polaire de la forme quadratique χ.
Remarque: Dans le cas des nombres complexes, il existe une autre forme disposant d'une linéarité différente et souvent plus intéressante, on parle alors de forme sesquilinéaire.
Par défaut, dans le reste de l'article E et F sont deux espaces vectoriels sur un même corps K et (.|.) désigne une forme bilinéaire. Une forme bilinéaire peut aussi être désignée par une lettre, par exemple b, alors (.|.)b désigne aussi cette forme bilinéaire.
Définitions associées à l'orthogonalité
En terme général, l'orthogonalité est un terme utilisé pour deux vecteurs x et y vérifiant la propriété (x|y) est nul. Elle généralise la notion de perpendicularité dans le cas d'un espace euclidien.
-
- Deux vecteurs x de E et y de F sont dit orthogonaux si et seulement si l'image du couple (x, y) par la forme bilinéaire est nulle.
-
- L'ensemble des vecteurs dont l'image avec tous les éléments d'une famille de vecteurs Φ est nulle est un espace vectoriel appelée orthogonal de Φ. Cet ensemble est souvent noté
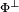 .
.
- L'ensemble des vecteurs dont l'image avec tous les éléments d'une famille de vecteurs Φ est nulle est un espace vectoriel appelée orthogonal de Φ. Cet ensemble est souvent noté
Si E est égal à F et que la forme bilinéaire n'est pas symétrique, pour éviter les confusions, on parle d'orthogonal à droite et à gauche. Un cas particulier, l'orthogonal du vecteur nul donne lieu à une définition spécifique.
-
- Le noyau à gauche d'une forme bilinéaire sur un espace ExF est l'ensemble des éléments x tel que :
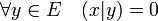
On définit de la même manière un noyau à droite.
Dans le cas où E et F sont confondus, il n'est pas nécessaire que la forme soit symétrique pour que les notions d'orthogonalité ou de noyaux à gauche ou à droite soit confondus, il suffit que la propriété donnant lieu à la définition suivante soit vérifiée :
-
- Une forme bilinéaire est dite réflexive si et seulement si la propriété suivante est vérifiée:
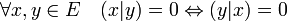
Définitions associées au cas où E est égal à F
Dans le cas ou E est égal à F, il existe des propriétés spécifiques pour les formes bilinéaires. Dans ce paragraphe, la forme linéaire est définie sur ExE.
-
- Une forme bilinéaire est dite symétrique si et seulement si la propriété suivante est vérifiée :

-
- Une forme bilinéaire est dite antisymétrique si et seulement si la propriété suivante est vérifiée :
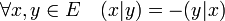
-
- Une forme bilinéaire est dite alternée si et seulement si la propriété suivante est vérifiée :
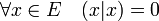
Toute forme alternée est antisymétrique. Si le corps n'est pas de caractéristique deux, alors les deux notions sont équivalentes. Dans le reste de l'article, le corps K est supposé est de caractéristique différente de deux.
-
- Une forme bilinéaire est dite dégénérée si et seulement si la propriété suivante est vérifiée :
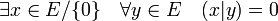
Pour les deux propriétés suivante, le corps K est supposé totalement ordonné, comme par exemple celui des réels.
-
- Une forme bilinéaire est dite positive si et seulement si la propriété suivante est vérifiée:
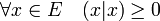
-
- Une forme bilinéaire est dite définie positive si et seulement si elle est positive et si la propriété suivante est vérifiée:
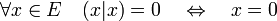
Une forme bilinéaire définie positive est donc non dégénérée.
Exemples
L'espace euclidien usuel
Article détaillé : Espace euclidien.L'espace R3 formé des triplets de nombres réels (x, y, z) peut être muni d'une forme bilinéaire nommée produit scalaire canonique. S'il est noté (.|.), il est défini par :
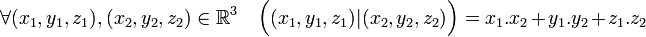
L'espace R3 muni de son produit scalaire est qualifié d'euclidien.
La forme bilinéaire duale
Un tel espace est équipé d'une autre forme bilinéaire importante définie à l'aide de l'espace dual R3* . Il correspond à l'ensemble des formes linéaires, c'est-à-dire les applications linéaires de R3* dans son corps de nombres R. Cette forme bilinéaire est l'application de R3*xR3, qui au couple (d *, x) associe <d *, x> désignant l'image de x par la forme linéaire d *. À certains égards, elle ressemble à l'exemple précédent.
Soit (e1, e2, e3) la base canonique de R3, notons di l'image <d *, ei> de ei par d * et d le vecteur de R3 (d1, d2, d3). La propriété suivante est vérifiée :
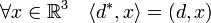
Il existe donc une certaine équivalence entre les deux formes bilinéaires et toute forme linéaire est représentée par un vecteur de R3 à l'aide du produit scalaire.
Remarque : La notation <d *, x>R3 désigne l'image de x par d * dans l'espace R3. Elle est appelée crochet de dualité. Quand il n'existe pas de risque d'ambiguité, le nom de l'espace vectoriel est omis. Cette notation est souvent utilisée pour la forme linéaire canonique entre un dual et son espace. On la trouve aussi dans la littérature pour désigner d'autres formes bilinéaires, comme des produits scalaires.
Un espace fonctionnel
Article détaillé : Espace préhilbertien.Considérons maintenant l'espace E des fonctions continues du segment [0, 1] dans R. Une forme bilinéaire joue un rôle clé sur E. Elle est définie de la manière suivante :

Encore une fois l'espace E possède l'autre forme bilinéaire, celle définie sur E*xE qui à tout couple d'un élément d * du dual de E et d'un élément f de E associe <d *, f> l'image par d * de f. Néanmoins la géométrie de E diverge de celle de l'exemple précédent. Soit δ la forme linéaire qui, à toute fonction f de E associe f(0). Elle correspond bien à un élément de E*, mais ne peut pas se représenter par une fonction de E. Une telle forme linéaire porte le nom de fonction δ de Dirac. En un sens, le dual de E est trop vaste pour pouvoir être représenté par les fonctions de E.
Il n'est pas étonnant que des différences de cette nature retentissent sur l'étude des formes bilinéaires.
Forme bilinéaire et application linéaire
Dual
Article détaillé : Espace Dual.Le dual E* est l'espace des formes linéaires de E dans K le corps sous-jacent de l'espace vectoriel E. Il existe une forme bilinéaire canonique sur E*xE. elle associe à tout couple formé d'un élément du dual f * et d'un élément x de l'espace, l'image du vecteur par la forme linéaire.
-
- La forme bilinéaire canonique sur E*xE est non dégénérée.
En effet par définition la seule forme linéaire nulle sur E est la forme nulle. Le noyau à gauche est donc réduit à la forme nulle. Si x est un vecteur non nul de E, il existe une forme linéaire qui vaut un en x et zéro sur un hyperplan supplémentaire de la droite engendrée par x. Le seul vecteur qui annule toutes les formes linéaires est donc le vecteur nul, ce qui montre que le noyau au droite est aussi réduit au vecteur nul.
Cette forme bilinéaire joue un rôle particulier, elle permet d'exprimer toutes les formes bilinéaires. Soit (.|.) une forme bilinéaire de ExF. Si x est un élément de E, alors ( x|. ) est un élément du dual de F. Soit φ1 l'application de E vers F*, qui à x associe la forme linéaire ( x|. ). On peut définir de même une application φ2 de F vers le dual de E. On dispose des égalités suivantes :
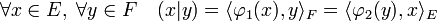
-
- Les applications φ1 et φ2 sont linéaires.
Cette propriété est la conséquence directe de la bilinéarité de la forme (.|.).
Noyau
La structure des applications φ1 et φ2 permettent de comprendre la géométrie des noyaux :
-
- Le noyau de φ1 (resp. φ2) est le noyau à gauche (resp. à droite) de la forme bilinéaire.
Le corollaire immédiat est que les noyaux à gauche et à droite sont des sous-espaces vectoriels.
Soient N1 (resp. N2) le noyau à gauche (resp. à droite) de la forme bilinéaire et M1 (resp. M2) des supplémentaires de N1 (resp. N2). Leur l'existence dans le cas général suppose l'utilisation de l'axiome du choix.
-
- La restriction de la forme bilinéaire à M1xM2 est non dégénérée. Le projecteur p1 (resp. p2) sur M1 (resp. M2) parallèlement à N1 (resp. N2) vérifie la propriété suivante :
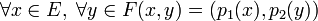
La forme bilinéaire se réduit à une forme non dégénérée une fois que les deux noyaux ont été retirés. Ce retrait permet toujours une détermination exacte de la forme bilinéaire. En dimension finie, la propriété suivante est vérifiée :
-
- La dimension de M1 est égale à celle de M2.
-
- La forme bilinéaire est non dégénérée si et seulement si φ1 est un isomorphisme. Alors φ2 est aussi un isomorphisme.
Démonstrations-
- La restriction de la forme bilinéaire à M1xM2 est non dégénérée et le projecteur p1 (resp. p2) sur M1 (resp. M2) parallèlement à N1 (resp. N2) vérifie la propriété suivante :
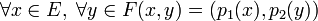
Pour tout élément m1 de M1 il existe un vecteur y de F non orthogonal à m1. En effet, cet élément n'est pas dans le noyau de la forme bilinéaire. Le vecteur y se décompose en somme d'un élément m2 de M2 et n2 de N2. On a alors :
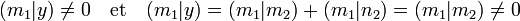
La dernière égalité montre que le noyau à gauche de la restriction est réduit au vecteur nul. Un raisonnement analogue montre que le noyau à droite est aussi réduit au vecteur nul.
La dernière propriété provient du fait que x - p1(x) (resp. y - p1(y)) est un élément du noyau à gauche (resp. à droite), en conséquence :
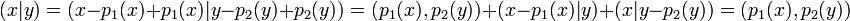
-
- La dimension de M1 est égale à celle de M2 :
Cette propriété est une conséquence de la proposition précédente. L'image par φ1 de M1 est incluse dans l'ensemble des formes bilinéaires de M2 sa dimension ne dépasse pas celle du dual de M2 et donc celle de M2 car en dimension finie un dual a même dimension que l'espace direct. L'application φ1 restreinte à M1 possède un noyau réduit au vecteur nul, en conséquence M1 a même dimension que son image par φ1. Ceci démontre que la dimension de M1 est inférieure ou égale à celle de M2. Le même raisonnement montre que la dimension de M2 est aussi inférieure ou égale à celle de M1, ce qui permet de conclure.
-
- La forme bilinéaire est non dégénérée si et seulement si φ1 est un isomorphisme, alors φ1 est aussi un isomorphisme :
Si la forme bilinéaire est non dégénérée alors les deux noyaux sont réduits au vecteur nul et les dimensions de E et de F sont égales d'après la proposition précédente. Alors φ1 est injectif car son noyau est réduit au vecteur nul et l'égalité des dimensions de E et du dual de F montre la surjectivité. Un raisonnement analogue montre que φ2 est aussi un isomorphisme.
Réciproquement si φ1 est un isomorphisme son noyau est réduit au vecteur nul, et l'image de φ1 est le dual entier de F. Un vecteur y de F orthogonal à tous les éléments de E est orthogonal au dual de F pour la forme <., .>F. Un seul vecteur vérifie cette propriété, le vecteur nul, en conséquence le noyau à droite est aussi réduit au vecteur nul, ce qui termine la démonstration.
Orthogonalité
La notion de noyau peut être étendue :
-
- L'ensemble des vecteurs dont l'image par la forme bilinéaire avec tous les éléments d'une famille de vecteurs Φ de E est nulle est un sous-espace vectoriel de F appelée orthogonal de Φ. Cet ensemble est souvent noté
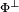 .
.
- L'ensemble des vecteurs dont l'image par la forme bilinéaire avec tous les éléments d'une famille de vecteurs Φ de E est nulle est un sous-espace vectoriel de F appelée orthogonal de Φ. Cet ensemble est souvent noté
L'orthogonal d'une famille de vecteurs de F est évidemment aussi un sous-espace vectoriel. Cet espace vectoriel contient le noyau à gauche de la forme bilinéaire. À l'aide de cette définition les noyaux apparaissent comme l'orthogonal des espaces E et F.
-
- L'orthogonal de
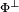 est un sous-espace vectoriel contenant celui engendré par Φ.
est un sous-espace vectoriel contenant celui engendré par Φ.
- L'orthogonal de
-
- Soit E1 et E2 deux sous-espaces vectoriels de E, alors l'orthogonal de la somme de E1 et E2 est l'intersection des orthogonaux. L'orthogonal de l'intersection est la somme des orthogonaux :
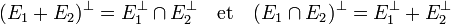
En dimension finie, on dispose de plus de l'égalité suivante :
-
- La dimension de
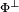 est la codimension de l'espace vectoriel engendré par Φ, si la forme bilinéaire est non dégénérée.
est la codimension de l'espace vectoriel engendré par Φ, si la forme bilinéaire est non dégénérée.
- La dimension de
Un corollaire de ce cas particulier indique que l'orthogonal de
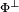 est la somme l'espace vectoriel engendré par Φ et le noyau à gauche de la forme bilinéaire. On remarque que l'application qui, à un sous-espace de E contenant le noyau à gauche ou de F contenant le noyau à droite, associe son orthogonal est involutive. Un autre corollaire indique que, si E est égal à F et si la forme est non dégénérée, alors l'orthogonal d'un sous-espace est un supplémentaire.Démonstrations
est la somme l'espace vectoriel engendré par Φ et le noyau à gauche de la forme bilinéaire. On remarque que l'application qui, à un sous-espace de E contenant le noyau à gauche ou de F contenant le noyau à droite, associe son orthogonal est involutive. Un autre corollaire indique que, si E est égal à F et si la forme est non dégénérée, alors l'orthogonal d'un sous-espace est un supplémentaire.Démonstrations-
- L'orthogonal de Φ est un sous-espace vectoriel de F :
L'orthogonal de Φ contient au moins le vecteur nul, il suffit de montrer qu'il est stable par combinaison linéaire pour démontrer cette proposition. Soit y1, y2 deux vecteurs de l'orthogonal de Φ, λ un scalaire et x un vecteur de la famille Φ :
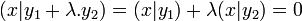
La dernière égalité montre la stabilité par combinaison linéaire et permet de conclure.
-
- L'orthogonal de
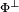 est un sous-espace vectoriel contenant celui engendré par Φ.
est un sous-espace vectoriel contenant celui engendré par Φ.
- L'orthogonal de
L'orthogonal de
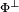 contient au moins le vecteur nul, il suffit de montrer qu'il est stable par combinaison linéaire. Soit x1, x2 deux vecteurs de l'orthogonal de
contient au moins le vecteur nul, il suffit de montrer qu'il est stable par combinaison linéaire. Soit x1, x2 deux vecteurs de l'orthogonal de 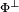 , λ un scalaire et y un vecteur de la famille
, λ un scalaire et y un vecteur de la famille 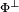 :
: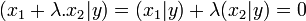
La dernière égalité et le fait que tout élément de Φ est orthogonal à tout élément de
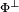 permet de conclure.
permet de conclure.-
- Soit E1 et E2 deux sous-espaces vectoriels de E, alors l'orthogonal de la somme de E1 et E2 est l'intersection des orthogonaux et l'orthogonal de l'intersection est la somme des orthogonaux : :
Tout vecteur de l'orthogonal de la somme E1 + E2 est à la fois orthogonal aux éléments de E1 et de E2, l'orthogonal de cette somme est donc incluse dans l'intersection des orthogonaux. Réciproquement tout vecteur de l'intersection est bien orthogonal à chaque vecteur de E1 et de E2 et donc à leur somme car l'orthogonal d'une famille est un sous-espace vectoriel.
La deuxième partie de la proposition se démontre de manière analogue.
-
- La dimension de
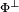 est la codimension de l'espace vectoriel engendré par Φ.
est la codimension de l'espace vectoriel engendré par Φ.
- La dimension de
Soit n la dimension de F et (f1*,..., fp*), où p est un entier strictement inférieur à n, une base de
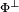 . Il est possible de compléter la base de
. Il est possible de compléter la base de 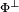 en une base (f1*,..., fn*) de F*. Soit (f1,..., fn) la base de F tel que (f1*,..., fn*) soit sa base duale, alors (fp+1,..., fn) est une base de l'orthogonal de
en une base (f1*,..., fn*) de F*. Soit (f1,..., fn) la base de F tel que (f1*,..., fn*) soit sa base duale, alors (fp+1,..., fn) est une base de l'orthogonal de 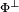 , ce qui démontre le résultat.
, ce qui démontre le résultat.Applications linéaires de l'espace vers le dual
Le paragraphe précédent montre l'existence d'une application canonique des formes bilinéaires de ExF vers l'espace des applications de E dans le dual F*. Soit (.|.)b une forme bilinéaire et ψ1b l'application, qui à x élément de E associe la forme linéaire de F (x|.)b. L'application ψ1, qui à (.|.)b associe ψ1b est une fonction de L2(ExF) dans L(E,F*). On définit de même une application ψ2 de L2(ExF) dans L(F,E*).
-
- L'ensemble des formes bilinéaires de ExF forme un espace vectoriel.
-
- L'application ψ1 (resp. ψ2) est un isomorphisme de L2(ExF) dans L(E,F*) (resp. L(F,E*).
Montrons que ψ1 est injective. Soit k un élément du noyau, alors ψ1k a pour image par tout vecteur de E la forme linéaire nulle, par définition d'un élément du noyau, l'application est donc bien injective. Elle est aussi surjective, en effet, soit f une application de L(E,F*), alors la forme bilinéaire qui au couple (x,y) associe <f(x), y> est un antécédent.
A la différence du paragraphe précédent, ce résultat ne tombe jamais en défaut, même en dimension infinie. Une forme bilinéaire b se représente ainsi par deux applications linéaires ψ1b et ψ2b. Elles sont liés par les égalités suivantes :
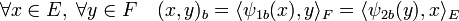
Les différents isomorphismes montrent que l'application qui à ψ1b associe ψ2b est un isomorphisme. On dit que ψ2b est l'application linéaire transposée de ψ1b. La définition est proche de celle plus topologique d'adjoint. L'application qui, à une application linéaire associe sa transposée, est un isomorphisme car composée d'isomorphismes.
En dimension finie, cette proposition possède le corollaire suivant :
-
- Si E et F sont de dimension finie alors la dimension de L2(ExF) est le produit des dimensions de E et de F.
Cette proposition découle directement du fait que la dimension de l'espace des applications linéaires d'un espace de dimension finie dans un espace de dimension finie.
Représentation matricielle
La dimension finie dispose d'une représentation pour offrir un mode opératoire simple des différents outils de l'algèbre linéaire : les matrices. Si leur origine provient surtout de la représentation d'applications linéaires, les isomorphismes du paragraphe précédent permettent de les utiliser pour les formes bilinéaires. Pour introduire ces outils une définition est utile, celle de base duale.
Si (ei) pour i variant de 1 à n est une base de E, il est possible de définir une base du dual particulièrement commode :
-
- La famille (ei* ) pour i variant de 1 à n et définie par <ei*, ej> = δij et une base de E* dite base duale de (ei).
Le symbole δij, appelé symbole de Kronecker désigne la fonction qui vaut un si i est égal à j et zéro sinon.
Si b (resp. a*) est un vecteur de E (resp. de E*) de coordonnées (bi) (resp. (ai)), alors l'égalité suivante est vérifiée :
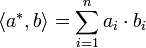
Soit F un deuxième espace vectoriel de base (fj), F* son dual, (fj*) la base duale associée et φ une forme bilinéaire de ExF, que l'on note (.,.)φ. Notons ici α l'image de φ par l'isomorphisme ψ1. Si (αji) la matrice A de α dans les bases (ei) et (fj*). La matrice tA de la transposée de l'application linéaire α est égale à (α'ij) avec α'ij = αji. Cette matrice est appelée matrice transposée de A et est souvent noté tA.
Soit x (resp. y) un vecteur de E (resp. F) de coordonnées (xi) (resp. (yj)) dans la base (ei) (resp. (fj)) et de matrice associée X (resp. Y), on obtient :
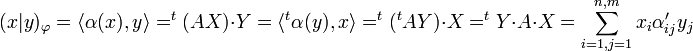
Si les outils et le mode calculatoire sont les mêmes que ceux des applications linéaires, la spécificité des formes bilinéaires apparait pour un changement de base. Soit P (resp. Q) la matrice de changement de base d'une nouvelle base dans (ei) (resp. fj) et X' (resp. Y' ) (resp. A' ) la matrice de x (resp. y) (resp. A) dans la nouvelle base, la formule devient :
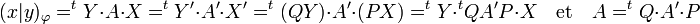
Produit tensoriel
Construction de formes bilinéaires
Si a* (resp. b*) est une forme linéaire de E (resp. de F), il existe une méthode simple de construire une forme bilinéaire sur ExF. Cette forme est notée a*
 b* et est définie par :
b* et est définie par :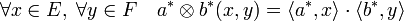
Cette opération s'appelle le produit tensoriel de a* et b*. L'espace E*
 F* désigne le sous-espace vectoriel de L2(E,F) engendré par l'image du produit tensoriel. Un vecteur x de E peut être identifié à une forme linéaire sur E*. En effet, à une forme linéaire a*, elle associe le scalaire <a*, x>. Cette remarque permet de considérer le produit tensoriel d'un élément de E et d'un élément de F qui est une forme bilinéaire sur E*xF*.
F* désigne le sous-espace vectoriel de L2(E,F) engendré par l'image du produit tensoriel. Un vecteur x de E peut être identifié à une forme linéaire sur E*. En effet, à une forme linéaire a*, elle associe le scalaire <a*, x>. Cette remarque permet de considérer le produit tensoriel d'un élément de E et d'un élément de F qui est une forme bilinéaire sur E*xF*.Le fait d'utiliser un espace ou son dual possède une signification profonde en physique. Pour cette raison, si l'ensemble de départ est un espace dual, les physiciens utilisent le terme de contravariant et dans le cas contraire de covariant. Le premier produit tensoriel présenté ici est deux fois contravariant.
Propriétés
L'image de E*xF* par le produit tensoriel n'est pas l'ensemble des formes bilinéaires de ExF, ce n'est pas non plus un espace vectoriel. En revanche il possède d'autres propriétés :
-
- L'application produit tensoriel de E*xF* dans L2(E, F) est bilinéaire, commutative.
-
- L'égalité suivante (E
 F)* = E*
F)* = E* F* est vérifiée.
F* est vérifiée.
- L'égalité suivante (E
-
- L'image de E*xF* par le produit tensoriel est un cône. Il est générateur de L2(E, F) si E et F sont de dimension finie.
Deux produits supplémentaires sont développés le produit extérieur et le produit symétrique. Appliqué à deux vecteurs a* et b* de E* on obtient :
- Produit symétrique :
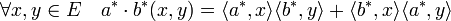
- Produit extérieur :
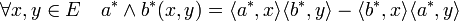
On obtient l'égalité :
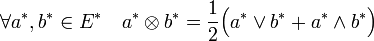
-
- Le produit extérieur (resp. symétrique) a son image incluse dans les formes bilinéaires alternées (resp. symétrique).
- Les espaces vectoriels engendrés par les produits extérieurs et symétriques sont en sommes directes. En dimension finie, le premier espace est de dimension n(n - 1)/2 et le deuxième n(n + 1)/2.
Démonstrations-
- L'application produit tensoriel de E*xF* dans L2(E, F) est bilinéaire :
C'est une conséquence immédiate de sa définition. Soit a* et b* deux vecteurs de E*, c* un vecteur de F* et λ un scalaire.
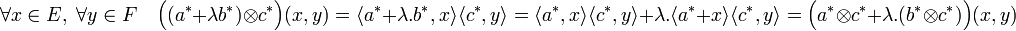
La commutativité se démontre de même.
-
- L'égalité suivante (E
 F)* = E*
F)* = E* F* est vérifiée :
F* est vérifiée :
- L'égalité suivante (E
En effet, (E
 F)* désigne le dual des formes bilinéaires sur E*xF*. Soit x (resp. y) un élément de E (resp. F) et α un élément de (E
F)* désigne le dual des formes bilinéaires sur E*xF*. Soit x (resp. y) un élément de E (resp. F) et α un élément de (E F)*. Soit φ l'application qui à α associe φα la forme bilinéaire sur ExF, c'est-à-dire l'élément de E*
F)*. Soit φ l'application qui à α associe φα la forme bilinéaire sur ExF, c'est-à-dire l'élément de E* F* suivant :
F* suivant :
L'application φα est manifestement biliénaire de ExF et φ est est linéaire.
Montrons qu'elle est injective : Si α est élément du noyau de φ, alors φα est nul sur une famille génératrice de E
 F et donc α est la forme nulle.
F et donc α est la forme nulle.Montrons qu'elle est surjective : Il suffit pour cela de montrer que si a* (resp. b*) est un élément du dual de E (resp. de F), alors a*
 b* possède un antécédent par φ.
b* possède un antécédent par φ.-
- L'image de E*xF* par le produit tensoriel est un cône :
Si a*, (resp. b*) est un élément de E* (resp. de F*) et Il suffit de remarquer que : Soit β l'élément de (E
 F)* défini par :
F)* défini par :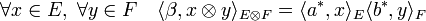
Alors, par construction φβ = a*
 b*, ce qui termine la démonstration.
b*, ce qui termine la démonstration.-
- L'image de E*xF* par le produit tensoriel est un cône :
Si b est une forme bilinéaire de E*xF*, alors il existe un vecteurs x* (resp. y*) de E* (resp. F*) tel que b est égal à x*
 y*. Si λ est un scalaire, alors λb est égal à (λx*)
y*. Si λ est un scalaire, alors λb est égal à (λx*) y* est fait partie de l'image du produit tensoriel.
y* est fait partie de l'image du produit tensoriel.-
- L'image de E*xF* par le produit tensoriel est générateur de L2(E, F) si E et F sont de dimension finie :
Soit n (resp. m) la dimension de E (resp. de F). Le théorème sur la dimension d'un espace d'applications linéaires montre que L(E, F*) est de dimension n.m. Si (ei*) (resp. (fj*)) est une base de E* (resp. de F*), la famille ei*
 fj* est libre et de même dimension que L(E, F*) qui est isomorphe à L2(E, F). Cette propriété montre que cette dernière famille est une base et démontre la proposition.
fj* est libre et de même dimension que L(E, F*) qui est isomorphe à L2(E, F). Cette propriété montre que cette dernière famille est une base et démontre la proposition.-
- L'ensemble des formes bilinéaires symétriques (respectivement antisymétriques) forme un sous-espace vectoriel. Ces deux sous espaces vectoriels sont en somme directe :
Le fait que la somme ou la multiplication scalaire soit stables pour les deux ensembles est évident. Ce sont donc des sous-espaces vectoriels.
L'égalité suivante montre que toute forme bilinéaire est la somme d'une forme symétrique et d'une antisymétrique. Leur somme engendre l'espace des formes bilinéaires:

L'intersection des deux sous-espaces est de manière évidente réduite à la forme nulle.
Complexifié d'un espace vectoriel
Un exemple simple correspond au complexifié d'un espace vectoriel réel. Si E désigne un espace vectoriel réel, de dimension finie ou non, et si C l'ensemble des nombres complexes considéré ici comme un espace vectoriel réel de dimension deux. Le corps C est identifié avec son dual avec l'application qui à un complexe λ associe l'application μ → Reλ.Reμ+Imλ.Imμ. Alors C
 E est l'espace vectoriel des formes bilinéaires de CxE* (la forme associée à E* est un élément de E identifié au bidual). l'espace CxE* est muni d'une multiplication naturelle sur C :
E est l'espace vectoriel des formes bilinéaires de CxE* (la forme associée à E* est un élément de E identifié au bidual). l'espace CxE* est muni d'une multiplication naturelle sur C :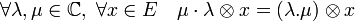
-
- Dans C
 E tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E.
E tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E.
- Dans C
-
- Si (ej) est une base de E, alors (1
 ei) est une base de C
ei) est une base de C E en tant que C espace vectoriel.
E en tant que C espace vectoriel.
- Si (ej) est une base de E, alors (1
Il est fréquent que E soit identifié à 1
 E, E est alors considéré comme un C espace vectoriel.Démonstrations
E, E est alors considéré comme un C espace vectoriel.Démonstrations-
- Dans C
 E tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E :
E tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E :
- Dans C
Soit b une forme bilinéaire de CxE*. Elle vérifie la proposition suivante :

donc
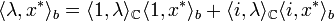
L'application qui à x* associe <1,x*> (resp. <i,x*>) est une forme linéaire que l'on note x1 (resp. xi). On obtient :
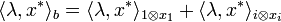
Ce qui termine la démonstration.
-
- Si (ej) est une base de E, alors (1
 ei) est une base de C
ei) est une base de C E en tant que C espace vectoriel.
E en tant que C espace vectoriel.
- Si (ej) est une base de E, alors (1
La démonstration est immédiate, la proposition précédente montre que tout élément de si y est un élément de C
 E, alors :
E, alors :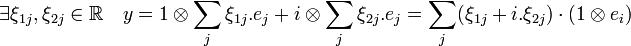
Dimension trois
Si E est un espace vectoriel de dimension trois, alors l'espace des formes bilinéaires alternées est aussi de dimension trois, car cet espace est de dimension n(n-1)/2. De même que le produit scalaire permet d'identifier un élément du dual avec un vecteur de l'espace, il est aussi possible d'identifier une forme bilinéaire alternée à un vecteur de E. L'application qui à trois vecteurs x, y, z associe le déterminant dans une base B : det (x, y, z)B est une application trilinéaire alternée. Cette application ne dépend pas du choix de la base, à condition qu'elle soit orthonormale et orienté. Elle prend le nom de produit mixte, il est noté [x, y, z]. Il permet d'identifier un vecteur c de E à la forme mc suivante :
![\forall x, y \in E \quad m_c(x,y)=[c,x,y]](/pictures/frwiki/55/77a08b0a3c83cb18840e1c81192bf40b.png)
Cette application m qui à un vecteur associe une forme bilinéaire alternée est un isomorphisme de E dans l'ensemble des formes bilinéaires alternée en dimension trois. À l'image de l'identification avec de E avec son dual grâce au produit scalaire. En dimension trois, les physiciens identifient E avec l'espace des formes bilinéaires alternées grâce à l'isomorphisme m. Ainsi, si a et b sont deux vecteurs de E et c le vecteur tel que a
 b est égal à mc, les physiciens écrivent :
b est égal à mc, les physiciens écrivent :![\forall a,b,c \in E \quad a\land b = c \Leftrightarrow \forall x,y \in E \quad a\land b(x,y) = [c,x,y]](/pictures/frwiki/54/6ea6c4964b7e9af16dd5cc54949b4ec0.png)
Si (.|.) désigne le produit scalaire de E, cette définition entraine :
![\forall x,y,z \in E \quad [x,y,z] = (x\land y| z)](/pictures/frwiki/48/0a42f7377828146eccabc7b1c1623ac7.png)
Espace vectoriel normé
Pour aller plus loin dans l'étude des formes bilinéaires dans le cas de la dimension infinie, une hypothèse supplémentaire est utile. Elle consiste à associer à l'espace vectoriel une topologie. Un cas particulier fréquent est celui où cette topologie dérive d'une norme conférant à l'espace une structure métrique. Cas particulier de formes bilinéaires est particulièrement étudié, celui où elles sont continues. Dans ce contexte, les isomorphismes généraux sont des isométries et la complétude naturelle du dual topologique apporte des propriétés fortes à l'espace des formes bilinéaires. Les relations d'orthogonalités se précisent si une hypothèse supplémentaire est faite sur les sous-espaces vectoriel : la fermeture.
Dans ce paragraphe, E et F désigne deux espaces vectoriels normés sur un corps K égal à R ou C et donc complet. La forme bilinéaire dont on parle par défaut est toujours notée (.|.).
Forme bilinéaire continue
La continuité des formes bilinéaires suit des règles proches de celles des opérateurs, terme généralement utilisé pour désigner les applications linéaires lorsque la dimension n'est pas finie.
-
- Les quatre propositions sont équivalentes :
-
- La forme bilinéaire est continue en tout point de ExF.
- La forme bilinéaire est continue en (0,0)
- L'image du produit cartésien des deux boules unités est bornée.
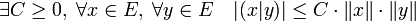
Les isomorphismes ψ1 et ψ2 offre une nouvelle condition nécessaire et suffisante pour la continuité de la forme bilinéaire :
-
- La forme bilinéaire b est continue si et seulement si ψ1b l'est. Alors ψ2b l'est aussi.
Si ψ2b est continue, il est alors évident que la forme bilinéaire et ψ1b le sont aussi.
-
- En dimension finie, toute forme bilinéaire est continue.
La situation est analogue à celle des opérateurs. En dimension finie, ils sont tous continus et dans le cas général, il existe une quadruple équivalence entre des propositions de la même nature que celles présentées ici.
-
- L'ensemble des formes bilinéaires continues est un sous-espace vectoriel de l'espace des formes bilinéaires.
Démonstrations-
- Si une forme bilinéaire est continue en (0,0) alors la proposition suivante est vraie :

Si la forme linéaire est continue alors elle l'est au point formé par les deux vecteurs nuls. Comme l'image de ce point par la forme bilinéaire est nulle, on obtient :

Ce qui peut encore s'écrire :

Cette dernière majoration prend la forme (1), si C est égal à ε/μ2.
-
- La proposition (1) est vraie si et seulement si l'image du produit cartésien des deux boules unités est bornée :
Si la proposition (1) est vraie, alors il suffit de constater que l'image du produit cartésien des deux boules unités est bornée par C.
Réciproquement si l'image du produit cartésien des deux boules unités est bornée par une constante C et si x (resp. y) désigne un vecteur non nul de E (resp. F), alors :
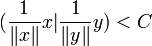
Et la proposition (1) est vraie.
-
- Si la proposition (1) est vraie, alors la forme bilinéaire est continue sur ExF :
Soit ε un réel strictement positif, (x0, y0) (resp. (h, k)) un point de ExF. La proposition (1) et la bilinéarité de la forme établissent que :

Soit μ le réel strictement positif égal au minimum de 1 et de ε/3C. Alors :
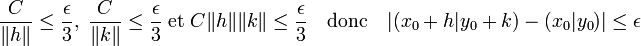
Ce qui démontre la continuité de la forme bilinéaire sur ExF.
Pour conclure il suffit de remarquer que la continuité de la forme bilinéaire sur ExF implique celle au point (0,0).
-
- La forme bilinéaire best continue si et seulement si ψ1b l'est. Alors ψ2b l'est aussi :
La proposition précédente montre que la forme bilinéaire est continue revient à dire que :

Dire que ψ1 est continue signifie que l'image de la boule unité de E est bornée dans F*. Autrement dit :
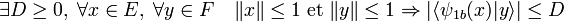
L'égalité entre la forme bilinéaire b et <ψ1b(.),.> permet de conclure.
-
- L'ensemble des formes bilinéaires continues est un sous-espace vectoriel de l'espace des formes bilinéaires :
Cette espace est en effet l'intersection du sous-espace vectoriel des formes continues et du sous-espace vectoriel des formes biliénaires sur ExF. L'espace vectoriel sous-jacent est celui des applications de ExF dans K.
Espace des formes bilinéaires continues
Le fait de munir E et F d'une norme et de limiter l'étude aux formes bilinéaires continues possède de multiple conséquences sur l'espace des formes bilinéaires. Dans ce paragraphe ne sont considérés que les applications linéaires, formes linéaires et formes bilinéaires continues.
-
- L'espace des formes bilinéaires sur ExF est normé par la norme des opérateurs.
Si suffit pour cela de définir la norme d'une forme bilinéaire de la borne supérieur de l'image de la valeur absolue ou du module de la forme bilinéaire sur le produit cartésien des deux boules unités.
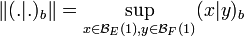
Ici BE(1) (resp. BF(1)) désigne la boule unité de rayon un de E (resp. de F). Pour s'en convaincre, il suffit de remarquer que cette norme est l'image de la norme des opérateurs de L(E, F*) par l'isomorphisme ψ1, en conséquence :
-
- L' application ψ1 (resp. ψ2) est une isométrie de L2(E,F;K) dans L(E,F*) (resp. L(F,E*)) si les espaces sont munis de la norme des opérateurs.
Si un espace est complet l'ensemble des applications linéaires continues dans cet espace est aussi complet (cette propriété est démontrée dans l'article Espace vectoriel normé). Comme K est complet L(F,K), c'est-à-dire F* l'est aussi. L'espace vectoriel des opérateurs de E vers F* munis de la normes des opérateurs est aussi complet, en conséquence :
-
- L'espace des formes bilinéaires sur ExF est complet.
Si F est complet et muni d'un produit scalaire (.|.), alors F est qualifié d'espace de Hilbert. Dans ce cas, le théorème de représentation de Riesz indique qu'il existe un isomorphisme isométrique entre F et son dual. C'est l'application qui à un vecteur x associe la forme (x|.), en conséquence :
-
- L'application qui à tout opérateur a de E vers F associe la forme bilinéaire noté (.|.)a suivante est un isomorphisme isométrique.
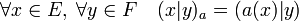
La configuration est la même qu'en dimension finie.
Orthogonalité
L'orthogonalité prend une forme un peu différente pour les espaces topologiques. Ici la forme bilinéaire est toujours continue. Soit Φ une famille de E, alors :
-
- L'orthogonal de Φ est un sous-espace vectoriel fermé de F.
En effet, soit (un) une suite de limite u d'élément de l'orthogonal de F et x un élément quelconque de Φ, la continuité de la forme bilinéaire montre que :
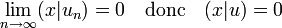
La dernière implication montre le caractère fermé de l'orthogonal de Φ. Sa structure d'espace vectoriel est déjà démontrée.
Un argument analogue à celui du paragraphe sur les orthogonaux montre que l'orthogonal de
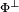 contient l'adhérence de la somme de l'espace vectoriel engendré par Φ et du noyau à gauche de la forme bilinéaire. Cependant, l'égalité n'est pas toujours vraie. Les égalités entre la somme et l'intersection d'othogonaux reste valable car la démonstration n'utilise aucune hypothèse sur la dimension.
contient l'adhérence de la somme de l'espace vectoriel engendré par Φ et du noyau à gauche de la forme bilinéaire. Cependant, l'égalité n'est pas toujours vraie. Les égalités entre la somme et l'intersection d'othogonaux reste valable car la démonstration n'utilise aucune hypothèse sur la dimension.Sources
Liens internes
Articles de mathématiques en rapport avec l'algèbre bilinéaireEspace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz
Liens externes
- (fr) Formes bilinéaires par les mathématiques.net. Ce site traite essentiellement de la dimension finie.
- (fr) Formes bilinéaires intégrales et opérateurs intégraux Par L. Schwartz. Cet exposé traite uniquement d'un cas de dimension infinie.
- (en) bilinear form par PlanetMath. Ce site suit un plan analogue à celui de l'article en plus succinct.
Références
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
- J.M. Arnaudiès et H. Fraysse Cours de mathématiques 4 : Algèbre bilinéaire et géométrie 1990 Dunod
- C. Semay B. Silvestre-Brac Introduction au calcul tensoriel, application à la physique Dunod 2007 (ISBN 978-2-10-050552-4)
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
- Portail des mathématiques
Catégorie : Algèbre bilinéaire -
Wikimedia Foundation. 2010.
