- Generateurs et relations dans le groupe du Rubik's Cube
-
Générateurs et relations dans le groupe du Rubik's Cube
Il est possible de faire une représentation mathématique du Cube de Rubik, un casse-tête qui fut en son temps très populaire. Cet article fait partie d'une série sur la théorie mathématique du Rubik's Cube.
Sommaire
Introduction
Notations utilisées
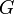 le groupe des mouvements légaux (sans démonter le cube !)
le groupe des mouvements légaux (sans démonter le cube !)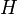 le groupe élargi (ici on peut faire sauter le cube)
le groupe élargi (ici on peut faire sauter le cube)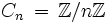
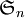 le groupe symétrique d'ordre n
le groupe symétrique d'ordre n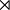 comme symbole pour le produit semi-direct
comme symbole pour le produit semi-direct pour la signature d'une permutation de
pour la signature d'une permutation de 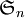
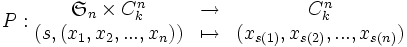
(où
 désigne
désigne 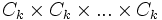 )
)- Les rotations d'un quart de tour dans le sens direct sont appelées
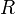 ,
,  ,
, 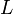 ,
, 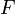 ,
,  ,
, 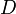 pour les faces
pour les faces
droite (right), haut (up), gauche (left), avant (front), arrière (back) et bas (down).
 l'opérateur de composition (avec
l'opérateur de composition (avec ![(f*g)(x) = g[f(x)] \,](/pictures/frwiki/55/753e80a958f6378a519ffe022e656e38.png) ).
).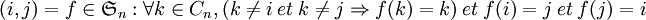
Présentation du problème
Définition d’un mot
Soit X un ensemble
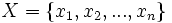 et un autre ensemble disjoint noté
et un autre ensemble disjoint noté  tel que pour tout élément de ces ensembles,
tel que pour tout élément de ces ensembles, 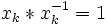 (élément neutre), avec
(élément neutre), avec 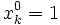 . Un mot est une séquence composée des éléments de
. Un mot est une séquence composée des éléments de 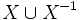 pondérés d’une puissance
pondérés d’une puissance 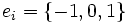 . Un mot s’écrit
. Un mot s’écrit 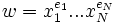 et le mot inverse est définit ainsi :
et le mot inverse est définit ainsi : 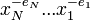 Un mot réduit est soit un mot vide (constitué que de 1) soit un mot pour lequel il n’y a pas deux symboles consécutifs de la forme
Un mot réduit est soit un mot vide (constitué que de 1) soit un mot pour lequel il n’y a pas deux symboles consécutifs de la forme 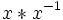 . Si
. Si  est un mot réduit, on définit alors la longueur de w par l(w) = N .
est un mot réduit, on définit alors la longueur de w par l(w) = N .Intérêt dans le Cube de Rubik
D’après les notations utilisées pour étudier le Cube, le problème peut se présenter sous deux formes. On peut le traiter en utilisant des notations totalement mathématiques ou alors le traiter sous forme de mots puisque chacune des lettres R,U etc. correspond à une permutation (voir numérotation du Cube). Il existe donc une fonction surjective de l’ensemble des mots sur X = {R,L,U,D,F,B} vers l’ensemble des permutations du Cube. Pour une permutation, la longueur est définie comme étant, en partant du Cube résolu, le nombre minimum de mouvement (= générateurs considérés) à effectuer pour obtenir la permutation.
Première application : nombre minimum de mouvements
À partir de ces mouvements, on peut construire un arbre où chaque nœud représente une position du cube (la permutation appliquée au cube résolu). En partant de l’identité, on peut construire une suite (Sn) qui à chaque étape est égal au nombre de position possible du cube réalisable avec n mouvements de base. On a S0 = 1,S1 = 18,S2 = 18 * 18 + 27 et ensuite pour tout n, on a Sn = 12Sn − 1 − 18Sn − 2. En effet, pour plus de précision dans le calcul, il ne faut pas compter toutes les permutations qui permettraient de revenir à une position déjà atteinte. Pour cela, il faut donc fixer des conditions (on compte ici les mouvements de la tranche du milieu) : on ne compte pas les positions obtenues par deux mouvements consécutifs sur une même face ni trois mouvements autour du même axe. Dans une situation donnée, il ne reste plus que 12 dans une position de Sn − 1 mouvements possible plus les 18 que l’on peut effectuer sur Sn − 2 qui correspond aux positions où l’on n’a pas répété les mouvements (ou encore les positions où l’on a répété les mouvements pour revenir à une identité). On peut ensuite calculer le terme général de la suite (Sn) puis l’égaler à N, le nombre de positions totales possibles du cube afin de déterminer n. On trouve alors n = 17.3 ce qui montre qu’il existe une position du cube qui ne peut pas être atteinte en moins de 18 mouvements. Il a même été prouvé qu'une position (le centre du cube) nécessite 20 mouvements.(Voir Optimal solutions for Rubik's Cube)
Générateurs et relations : présentation d’un groupe
Le groupe libre sur les générateurs éléments de X , noté FX est le groupe des mots réduits de X.
Dem :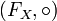 est un groupe :
est un groupe :- la loi
 est interne au groupe (la loi
est interne au groupe (la loi  étant définie comme la loi de composition avec en plus une réduction du mot obtenu)
étant définie comme la loi de composition avec en plus une réduction du mot obtenu) - admet un élément neutre 1
- associatif (loi de composition sur les permutations)
- un mot
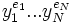 est inversible d’inverse
est inversible d’inverse 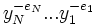 .
.
Définition : on appelle H sous groupe normal à G si pour tout g de G, on a g − 1 * H * g = H.
Soit X un ensemble fini avec n = card X. Soit Y un groupe de mots réduits sur X. Soit R le plus petit sous groupe normal de Fn contenant Y. R constitue l’ensemble des relations de Fn.
Dem : Fn/R est un groupe, c’est le plus grand groupe qui satisfait ces relations. Avec les notations précédentes, (G, o ) est par définition un groupe satisfaisant les relations de R (groupe quotient sur Fn) Soit G’ un autre groupe construit sur les mêmes générateurs X satisfaisant les relations de R. On considère
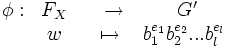 (qui à un mot w lui associe sa décomposition selon les générateurs de G’). Cette application est un morphisme de groupe avec
(qui à un mot w lui associe sa décomposition selon les générateurs de G’). Cette application est un morphisme de groupe avec  puisque G’ satisfait les relations de R donc f(R) = 1. D’après les théorèmes sur les morphismes, G est une extension de G’ donc G est le plus grand groupe généré par X satisfaisant les relations de R. Soit G un groupe. On dit que G a pour générateurs l’ensemble X et pour relations Y si G est isomorphe à Fn / R. Un ensemble de générateurs et de relations est appelé une présentation. En termes de notation, un élément r de R est noté sous forme d’une équation de la forme r = 1.
puisque G’ satisfait les relations de R donc f(R) = 1. D’après les théorèmes sur les morphismes, G est une extension de G’ donc G est le plus grand groupe généré par X satisfaisant les relations de R. Soit G un groupe. On dit que G a pour générateurs l’ensemble X et pour relations Y si G est isomorphe à Fn / R. Un ensemble de générateurs et de relations est appelé une présentation. En termes de notation, un élément r de R est noté sous forme d’une équation de la forme r = 1.Ex : le groupe cyclique d’ordre n possède un générateur x et une relation xn = 1 donc on a X = {x} et
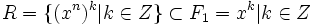 .Cn admet donc comme présentation: Cn = x | xn = 1 Le groupe diédral d’ordre n a pour présentation Dn = {a,b | an = 1,b2 = 1,aba = b}
.Cn admet donc comme présentation: Cn = x | xn = 1 Le groupe diédral d’ordre n a pour présentation Dn = {a,b | an = 1,b2 = 1,aba = b}Produit semi–direct
Définition
Produit direct de deux groupes : en considérant deux groupes G et H, le produit direct de G et de H est l’ensemble des couples (a,b) muni d’une loi produit telle que (a,b) * (a',b') = (a * a',b * b'). Si « G agit sur H », c'est-à-dire s'il existe un morphisme s de G dans A et H, on peut considérer la loi (a,b) * (a',b') = (a * s(b)(a'),b * b').
Cas du groupe G : l’intérêt d’une présentation pour ce groupe est que l’on peut établir un isomorphisme entre G et
 avec comme morphisme P présenté en introduction.
avec comme morphisme P présenté en introduction.Recherche d’une présentation de
Il faut d’abord chercher les représentations des groupes symétriques et des groupes cycliques. Pour le groupe symétrique d’ordre n+1, on a:
 avec
avec 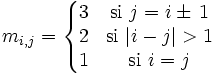 Dans le cas où n=4, la matrice est :
Dans le cas où n=4, la matrice est : 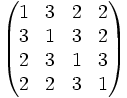
Pour le produit cartésien du groupe cyclique d'ordre m, on a :
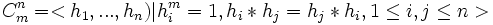
Pour le groupe symétrique, on peut associer à chaque transposition (de deux indices consécutifs) ai une matrice de permutation de taille (n+1)*(n+1)
 autrement dit si = I − Eii − Ei + 1,i + 1 + Ei,i + 1 + Ei + 1,i
autrement dit si = I − Eii − Ei + 1,i + 1 + Ei,i + 1 + Ei + 1,iOn peut aussi identifier
 avec le produit cartésien
avec le produit cartésien 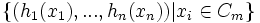 où hi(t) = I − Eii − Ei + 1,i + 1 + tEii + t − 1Ei + 1,i + 1
où hi(t) = I − Eii − Ei + 1,i + 1 + tEii + t − 1Ei + 1,i + 1On a alors les relations suivantes entre les siet les hj(t)
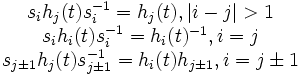
On peut alors démontrer la propriété suivante :
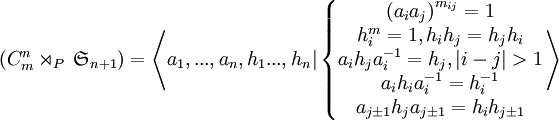
Démonstration : si on appelle P la représentation présentée ci-dessus. Le but de la démonstration est bien sûr de montrer
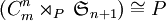 . Pour celà on considère le morphisme
. Pour celà on considère le morphisme 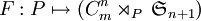 qui associe les générateurs de
qui associe les générateurs de  avec les générateurs de
avec les générateurs de 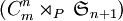 . Par définition de l'application,
. Par définition de l'application, 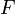 est surjective. Pour prouver l'injectivité, on note K = ker(F). En notant card(G) = | G | , on a d'après le théorème de Lagrange :
est surjective. Pour prouver l'injectivité, on note K = ker(F). En notant card(G) = | G | , on a d'après le théorème de Lagrange : 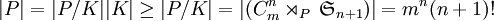 .
.En considérant maintenant
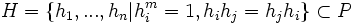 ,
, 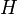 est un sous groupe normal à
est un sous groupe normal à  . En effet, chaque ai renvoie un générateur de H sur un produit de générateurs de H ou sur son inverse. Comme H est un groupe, on obtient que
. En effet, chaque ai renvoie un générateur de H sur un produit de générateurs de H ou sur son inverse. Comme H est un groupe, on obtient que  . On a donc
. On a donc 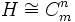 . Si w = W(a1,...,an,h1,...,hn) = 1 est une relation de P, le mot
. Si w = W(a1,...,an,h1,...,hn) = 1 est une relation de P, le mot  écrit dans le groupe quotient P / H devient un mot qui ne contiendra plus que des relations du type
écrit dans le groupe quotient P / H devient un mot qui ne contiendra plus que des relations du type  . On peut montrer ainsi que
. On peut montrer ainsi que  (cette partie de la démonstration sera précisée).
(cette partie de la démonstration sera précisée).Ainsi, on a
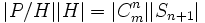 ce qui montre
ce qui montre  et ainsi
et ainsi  d'où
d'où  .
. 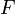 est donc injectif donc bijectif.
est donc injectif donc bijectif.Application
Dans le cadre de Caml A) Recherche d’un groupe de générateurs du Cube autre que les 6 usuels
On peut montrer que en réalité, on n’a besoin que de 5 car le 6e peut s’exprimer en fonction des 5 autres. Peut-on trouver un ensemble encore plus petit ? Mouvements de Barns : montrer avec le programme de Guix que l'on peut retrouver les mouvements de bases RU etc.
Dénombrement du groupe à partir des relations du produit semi direct
Liens externes
- Portail des mathématiques
- Portail des jeux
Catégories : Rubik's Cube | Théorie des groupes
Wikimedia Foundation. 2010.
