- Espace Topologique
-
Espace topologique
La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un contexte général pour traiter des notions de limite, de continuité, dans le cadre d'un continuum ou d'un espace discret, voire fini. Dans ce contexte, les espaces topologiques forment le socle conceptuel dans lequel ces notions sont définies. Le cadre est suffisamment général pour s'appliquer à un grand nombre de situations différentes : ensembles finis, discrets, espaces de la géométrie euclidienne, espaces numériques à n dimensions, espaces fonctionnels les plus complexes et géométrie algébrique. Ces concepts apparaissent dans presque toutes les branches des mathématiques ; ils sont donc centraux dans la vision moderne des mathématiques. La branche des mathématiques qui étudie ces espaces s'appelle la topologie.
La topologie générale ne tente pas d'élucider la question très complexe de la « composition du continu » : elle part d'une approche axiomatique, en utilisant le vocabulaire de la théorie des ensembles ; autrement dit, elle suit une approche fondée sur une notion de structure (en l'occurrence, ici, une structure topologique), en faisant usage d'une axiomatique ensembliste. Les axiomes sont minimaux, et en ce sens c'est la structure la plus générale pour étudier les concepts cités. Ils ont été formalisés par Kolmogorov au début du XXe siècle.
La topologie générale, en elle même, s'attache à définir le vocabulaire. Elle possède deux branches importantes : la topologie différentielle et la topologie algébrique, où la notion générale de « forme » est étudiée avec un degré de complexité et d'approfondissement extrêmes.
Cet article est technique, une vision générale et historique est donnée dans Topologie.
Sommaire
Concepts
Définitions
Un espace topologique est un couple (E,Τ), où E est un ensemble et Τ un ensemble de parties de E que l'on définit comme les ouverts de (E,Τ), vérifiant les propriétés suivantes :
- L'ensemble vide et
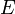 appartiennent à Τ.
appartiennent à Τ. - Toute réunion d'ouverts est un ouvert, c'est-à-dire si
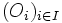 est une famille (finie ou infinie, dénombrable ou non dénombrable) d'éléments de Τ, alors
est une famille (finie ou infinie, dénombrable ou non dénombrable) d'éléments de Τ, alors
-
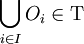 .
.
- Toute intersection finie d'ouverts est un ouvert, c'est-à-dire si
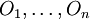 sont des éléments de Τ, alors
sont des éléments de Τ, alors
-
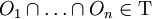 .
.
L'ensemble Τ, qui est un ensemble de parties de E, est alors appelé topologie de E.
Un fermé d'une topologie est défini comme le complémentaire d'un ouvert. Par conséquent, la famille des fermés contient E et l'ensemble vide. Il résulte de la théorie élémentaire des ensembles que toute intersection de fermés est un fermé et que toute réunion finie de fermés est un fermé.
Il est d'usage de rappeler la présence de la partie vide à l'axiome 1 ; c'est toutefois en toute rigueur superflu, puisqu'on peut l'obtenir en appliquant l'axiome 2 à la réunion indexée par l'ensemble vide.
Un des premiers rôles de la topologie est de décrire les voisinages des points. C'est une notion-clé pour comprendre la topologie. Elle sert par exemple à la définition de continuité ou de limite en un point. Cette notion est formalisée dans l'article voisinage. Rappelons ici simplement qu'une partie de E est un voisinage d'un point si elle contient un ouvert contenant ce point.
Exemples
- Un exemple simple est
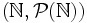 . Tous les singletons étant des ouverts, tous les points sont isolés les uns des autres. La topologie ainsi définie est appelée topologie discrète. Plus généralement, la topologie discrète sur un ensemble
. Tous les singletons étant des ouverts, tous les points sont isolés les uns des autres. La topologie ainsi définie est appelée topologie discrète. Plus généralement, la topologie discrète sur un ensemble  est celle pour laquelle
est celle pour laquelle  . En contrepartie de la simplicité, elle n'offre pas beaucoup d'intérêt.
. En contrepartie de la simplicité, elle n'offre pas beaucoup d'intérêt.
- La topologie grossière sur
 est celle pour laquelle les seuls ouverts sont la partie vide et
est celle pour laquelle les seuls ouverts sont la partie vide et 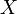 lui-même.
lui-même.
- Un exemple sur les entiers est
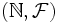 où
où 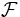 désigne le filtre de Fréchet, c'est-à-dire tous les complémentaires d'ensembles finis et l'ensemble vide. Cette topologie donne un sens au voisinage de l'infini et permet par exemple de définir la notion de limite d'une suite.
désigne le filtre de Fréchet, c'est-à-dire tous les complémentaires d'ensembles finis et l'ensemble vide. Cette topologie donne un sens au voisinage de l'infini et permet par exemple de définir la notion de limite d'une suite.
- L'article sur les voisinages démontre qu'il existe une topologie associée à tout espace métrique. Un ouvert
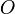 est alors un ensemble qui contient, pour chaque point
est alors un ensemble qui contient, pour chaque point 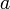 de
de 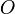 , une boule ouverte de centre
, une boule ouverte de centre 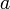 .
.
- L'ensemble des nombres réels est donc muni naturellement d'une topologie issue de sa distance. Un ouvert est alors une union d'intervalles ouverts.
- La topologie produit est une topologie définie sur un produit cartésien d'espaces topologiques. Un exemple est donnée par les espaces vectoriels de dimension finie réels ou complexes.
- La topologie induite d'un sous-ensemble
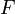 d'un ensemble
d'un ensemble 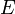 est la topologie obtenue par intersection des ouverts de
est la topologie obtenue par intersection des ouverts de 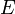 avec
avec 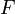 . Cette définition permet par exemple de définir la topologie induite par celle de
. Cette définition permet par exemple de définir la topologie induite par celle de  sur un intervalle, et ainsi de pouvoir définir les propriétés de continuité et de limite à des fonctions définies sur un intervalle de
sur un intervalle, et ainsi de pouvoir définir les propriétés de continuité et de limite à des fonctions définies sur un intervalle de  .
.
- D'autres exemples de topologies plus sophistiquées sont donnés dans l'article voisinage.
- Le cube de Hilbert
![[0,1]^\N](/pictures/frwiki/56/87018ac4548501371d4f40dc5e7d0c8f.png) est une généralisation du cube en dimension infinie.
est une généralisation du cube en dimension infinie.
- L'ensemble de Cantor est source de nombreux exemples et contre-exemples.
Topologie engendrée par une fonction
- Soient X un espace quelconque, Y un espace topologique et f une fonction de X dans Y. On peut alors définir sur X une topologie particulière liée à ce système. C'est la plus petite topologie (ou la plus grossière) sur X rendant f continue.
- De même, si f était de Y dans X, on définirait sur X la topologie la plus grande (ou la plus fine) telle que f soit continue.
On peut généraliser ces deux définitions en remplaçant Y par une famille, indéxée par I,
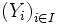 et f par
et f par 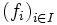 .
.Exemples
- La topologie induite peut être définie ainsi. Soit X inclus dans Y. On prend pour f l'identité de X dans Y.
- La topologie produit.
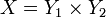 et
et 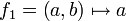 et
et 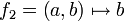 les deux projections associées. La topologie produit sur X est alors définie comme la topologie engendrée par ces deux projections.
les deux projections associées. La topologie produit sur X est alors définie comme la topologie engendrée par ces deux projections.
- La topologie faible. Soit E un espace vectoriel topologique et E' son dual topologique (l'ensemble des formes linéaires continues). Alors on définit sur E la topologie faible ainsi : on le munit de la topologie engendrée par les formes linéaires.
Applications continues
Définitions
Un des premiers intérêts de la notion d'espace topologique est de pouvoir définir une application continue. Il existe deux approches, l'approche locale donnée dans l'article voisinage et qui définit la continuité en un point, et l'approche globale qui définit la continuité en tout point.
- Définition globale. Une application
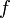 de
de 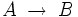 entre deux espaces topologiques est dite continue si l'image réciproque
entre deux espaces topologiques est dite continue si l'image réciproque 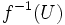 de tout ouvert
de tout ouvert  de
de 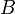 est un ouvert de
est un ouvert de 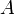 (l'image réciproque
(l'image réciproque 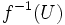 est l'ensemble de tous les points de
est l'ensemble de tous les points de 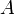 que
que 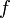 envoie dans
envoie dans  ).
).
- Définition locale. Soit
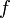 une fonction d'un espace topologique
une fonction d'un espace topologique 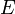 dans
dans 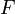 et soit
et soit 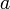 un point élément du domaine de définition de
un point élément du domaine de définition de 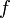 . La fonction
. La fonction 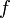 est continue au point
est continue au point 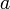 si et seulement si l'image réciproque d'un ouvert contenant
si et seulement si l'image réciproque d'un ouvert contenant  contient un ouvert contenant
contient un ouvert contenant 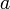 . Cet énoncé est équivalent à celui donné dans l'article voisinage.
. Cet énoncé est équivalent à celui donné dans l'article voisinage.
- Équivalence de la continuité locale en tout point et de la continuité globale. Si une application est globalement continue, l'image réciproque d'un ouvert contenant
 contient elle-même qui est un ouvert contenant
contient elle-même qui est un ouvert contenant 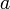 . L'application est donc continue en tout point. Réciproquement, si l'application est continue en tout point alors son image réciproque contient pour chaque point un ouvert le contenant et inclus dans l'image réciproque. L'union de tous ses ouverts est par définition un ouvert et est égal à l'image réciproque. L'image réciproque est donc ouverte.
. L'application est donc continue en tout point. Réciproquement, si l'application est continue en tout point alors son image réciproque contient pour chaque point un ouvert le contenant et inclus dans l'image réciproque. L'union de tous ses ouverts est par définition un ouvert et est égal à l'image réciproque. L'image réciproque est donc ouverte.
Une application bijective continue et dont la réciproque est continue est appelée un homéomorphisme.
Article détaillé : Continuité.Exemples
- L'application identité d'un espace topologique dans lui-même est continue. En effet l'image réciproque de tout ouvert est lui-même donc est ouvert.
- Une application constante d'un espace topologique dans un autre est continue. En effet l'image réciproque est soit l'ensemble vide soit l'ensemble de départ tout entier.
- l'application
 est continue. La preuve en est donnée dans l'article continuité.
est continue. La preuve en est donnée dans l'article continuité.
- Soit un espace X munie d'une topologie,
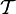 , quelconque, on le notera
, quelconque, on le notera 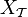 . On appelle
. On appelle 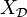 X muni de la topologie discrète,
X muni de la topologie discrète, 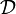 , et
, et 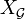 de la topologie grossière,
de la topologie grossière, 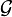 . Alors il existe les bijections continues (dont l'inverse n'est pas continue, sauf exceptions)
. Alors il existe les bijections continues (dont l'inverse n'est pas continue, sauf exceptions) 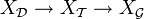 . La première étant d'inverse continu quand
. La première étant d'inverse continu quand 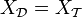 (
(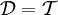 ) et la seconde quand
) et la seconde quand 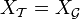 (
( ).
).
- Soit l'espace de Sierpinski Ω (le couple {0,1} muni de la topologie
 ). Soit X un espace topologique, alors pour chaque fonction continue de X dans Ω on a un ouvert de X donné par l'image réciproque de {1} et pour chaque ouvert de X une fonction continue de X dans Ω qui vaut 0 sur le complémentaire de l'ouvert et 1 sur l'ouvert. On obtient ainsi une bijection entre les fonctions continues de X dans Ω et les ouverts de X.
). Soit X un espace topologique, alors pour chaque fonction continue de X dans Ω on a un ouvert de X donné par l'image réciproque de {1} et pour chaque ouvert de X une fonction continue de X dans Ω qui vaut 0 sur le complémentaire de l'ouvert et 1 sur l'ouvert. On obtient ainsi une bijection entre les fonctions continues de X dans Ω et les ouverts de X.
- Même exemple que juste au-dessus, mais on munit le couple
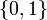 et X de leurs topologies discrètes. Ainsi on a une bijection entre les parties de X et les fonctions continues de X dans
et X de leurs topologies discrètes. Ainsi on a une bijection entre les parties de X et les fonctions continues de X dans 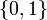 .
.
Limite
Adhérence
Cette notion est développée dans un article spécifique Adhérence. Nous ne développerons cette notion que dans la mesure où elle est nécessaire pour formaliser la notion de limite.
En topologie, l'adhérence d'une partie X d'un espace topologique est le plus petit ensemble fermé qui contient cette partie. On la note souvent
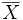 .
.Une autre façon de définir les espaces topologiques consiste à faire appel à la notion prétopologique d'adhérence : on définit une adhérence sur un ensemble E comme une application qui à toute partie A de E associe une partie contenant A, l'adhérence de la partie vide restant vide. Dans le cas où l'adhérence est idempotente et où l'adhérence de l'union de deux parties est égale à l'union des adhérences, on dit que l'adhérence est topologique. Un espace topologique peut se définir comme un ensemble muni d'une adhérence topologique. Les ouverts sont alors les complémentaires des parties stables pour l'adhérence.
En termes d'adhérences, une application d'un espace topologique dans un autre est continue si et seulement si l'image d'un point adhérent à une partie est nécessairement adhérente à l'image de cette partie.
Définition
La notion de limite en un point, si elle existe, décrit le comportement qu’une fonction devrait avoir si elle était définie en ce point. L’exemple le plus simple est le cas d’une fonction définie sur un intervalle ouvert de
 ; la limite est le concept qui permet de déterminer le comportement de la fonction aux bornes de cet intervalle.
; la limite est le concept qui permet de déterminer le comportement de la fonction aux bornes de cet intervalle.Soit
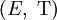 et
et 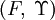 deux espaces topologiques. Soit
deux espaces topologiques. Soit 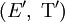 un sous-espace de
un sous-espace de 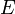 muni de sa topologie induite et
muni de sa topologie induite et 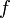 une fonction de
une fonction de 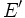 dans
dans 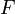 . Soit enfin un point
. Soit enfin un point 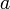 de
de 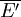 et
et 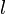 un point de
un point de 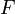 . Alors
. Alors 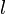 est la limite de la fonction
est la limite de la fonction 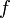 au point
au point 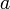 si et seulement si l’image réciproque d’un ouvert contenant
si et seulement si l’image réciproque d’un ouvert contenant 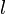 contient un ouvert de
contient un ouvert de 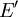 contenant
contenant 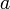 . Cet énoncé est équivalent à celui qui est donné dans l’article voisinage. L’énoncé étant plus simple avec le formalisme des voisinages, c’est en général celui-là qui est utilisé.
. Cet énoncé est équivalent à celui qui est donné dans l’article voisinage. L’énoncé étant plus simple avec le formalisme des voisinages, c’est en général celui-là qui est utilisé.- Remarque 1
- La notion de limite est développée dans l’article Limite.
- Remarque 2
- Si le point
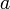 est élément de l’ensemble
est élément de l’ensemble 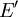 , alors la limite, si elle existe, est égale à
, alors la limite, si elle existe, est égale à  et la fonction
et la fonction 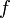 est continue en
est continue en 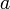 .
.
Propriétés
- On dit qu’un espace topologique est séparé ou de Hausdorff ou T2 lorsque deux points distincts quelconques admettent des voisinages disjoints.
- On dit qu’un espace vérifie la propriété de Borel-Lebesgue lorsqu’on peut extraire un sous-recouvrement fini de tout recouvrement ouvert. On parle aussi d’espace quasi-compact.
- Un espace quasi-compact et séparé est dit compact.
Exemples
- Le premier exemple historique d’espace topologique est l’ensemble des nombres réels. Cet exemple est celui qui est à la base de la théorie des espaces topologiques. Il apparaît comme un cas particulier de la deuxième famille d’exemples donnés ici.
- Les espaces métriques et, en particulier, les espaces vectoriels normés sont des espaces topologiques.
- Il existe de nombreuses classes d'espaces topologiques (espaces vectoriels topologiques, espace de Banach, de Fréchet, de Hilbert, de Hausdorff, de Kolmogorov, de Montel, de Baire, compacts, quasi-compacts, précompacts, paracompacts, bien enchaînés, complets, connexes, simplement connexes, connexes par arcs, localement compacts, localement connexes, groupe topologique, anneau topologique, etc.).
Voir aussi
- Portail des mathématiques
Catégories : Topologie | Topologie générale - L'ensemble vide et
Wikimedia Foundation. 2010.
