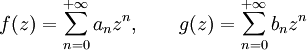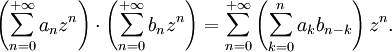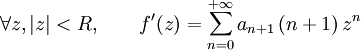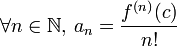- Serie entiere
-
Série entière
 Pour les articles homonymes, voir Entier (homonymie).
Pour les articles homonymes, voir Entier (homonymie).En mathématiques et particulièrement en analyse, une série entière est une série de fonctions de la forme
où les coefficients an forment une suite réelle ou complexe. La série est dite entière du fait qu'elle fait intervenir des puissances entières.
Les séries entières possèdent des propriétés de convergence remarquables, qui s'expriment pour la plupart à l'aide d'une grandeur associée à la série, son rayon de convergence R. Sur le disque de convergence (disque ouvert de centre 0 et de rayon R), la fonction somme de la série peut être dérivée indéfiniment terme à terme.
Réciproquement, certaines fonctions indéfiniment dérivables peuvent être écrites au voisinage d'un de leurs points c comme somme d'une série entière de la variable z-c : celle-ci est alors leur série de Taylor. On parle dans ce cas de fonctions développables en série entière au point c. Lorsqu'une fonction est développable en série entière en chacun de ses points, elle est dite analytique.
Les séries entières apparaissent en analyse, mais aussi en combinatoire en tant que fonction génératrice et se généralisent dans la notion de série formelle. Dans la théorie des nombres, le concept de nombre p-adique est proche de celui de série entière.
Sommaire
Définitions
Dans ce qui suit, la variable z est réelle ou complexe.
Série entière
Une série entière de variable z, est une série de terme général
 , où n est un entier naturel, et
, où n est un entier naturel, et 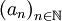 est une suite de nombres réels ou complexes. L'usage veut que l'on adopte la notation
est une suite de nombres réels ou complexes. L'usage veut que l'on adopte la notation 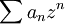 ou
ou 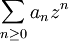 pour parler d'une série entière, tandis que l'on écrira
pour parler d'une série entière, tandis que l'on écrira 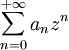 pour son éventuelle somme, en cas de convergence, pour un z donné.
pour son éventuelle somme, en cas de convergence, pour un z donné.Rayon de convergence
Article détaillé : Rayon de convergence.Une bonne partie des propriétés de convergence de la série peut être exprimée à l'aide de la quantité suivante, appelée rayon de convergence de la série
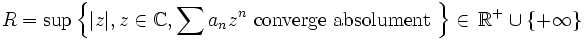 .
.
Ces propriétés se fondent sur le lemme suivant, dû à Abel, mais qu'il ne faut pas confondre avec le théorème d'Abel, lequel est utilisé pour démontrer la continuité de la somme de la série à la frontière du disque de convergence.
Lemme d'Abel — Soit un réel r0 > 0. Si la suite de terme général
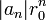 est bornée, alors la série
est bornée, alors la série  converge absolument pour | z | < r0.Démonstration
converge absolument pour | z | < r0.DémonstrationSi | z | < r0, alors
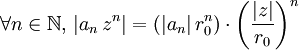 .
.
Le premier des termes de ce produit est borné, le second forme une série géométrique de raison strictement inférieure à 1. Par comparaison de séries à termes positifs, la conclusion s'ensuit.
Dès lors, il est possible de préciser le mode de convergence de cette série de fonctions
- La série entière converge absolument pour tout complexe z de module strictement inférieur au rayon. Le disque ouvert de centre 0 et de rayon R est appelé disque ouvert de convergence.
- La série diverge grossièrement (c'est-à-dire que le terme général ne converge pas vers 0) pour tout complexe z de module strictement supérieur au rayon.
- Pour tout réel r strictement inférieur au rayon, il y a convergence normale sur le disque fermé de centre 0 et de rayon r.
Dans le cas où la variable x est réelle, on parle encore de disque ouvert de convergence, bien que cela désigne un intervalle de la droite réelle (] − R; + R[).
Lorsque le rayon est infini, le disque ouvert de convergence est l'ensemble du plan complexe (ou de la droite réelle). En revanche il n'y a a priori convergence normale que sur les disques fermés de rayon fini. Un rayon nul signifie en revanche qu'il y a divergence en tout point autre que z=0, comme c'est le cas par exemple pour la série
 .
.Ces propriétés ne règlent pas toutes les questions de convergence. Notamment, aux points de module R, il peut y avoir convergence ou non, et convergence avec ou sans absolue convergence. Par exemple, les séries entières
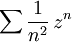 ,
, 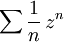 et
et 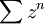 ont pour rayon de convergence 1, la série entière
ont pour rayon de convergence 1, la série entière 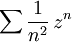 converge absolument en tout point de module 1 alors que
converge absolument en tout point de module 1 alors que 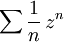 ne converge absolument en aucun point de module 1 mais converge en tout point autre que 1 et la série entière
ne converge absolument en aucun point de module 1 mais converge en tout point autre que 1 et la série entière 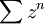 ne converge en aucun point de module 1.
ne converge en aucun point de module 1.Calcul du rayon de convergence
La formule de Hadamard donne l'expression du rayon de convergence en termes de limite supérieure
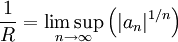 .
.
Cette formule découle de l'application de la règle de Cauchy.
Dans la pratique, si les an sont non nuls, il est parfois possible d'appliquer la règle de d'Alembert :
- Si
 (limite éventuellement infinie), alors le rayon de convergence est égal à 1/L.
(limite éventuellement infinie), alors le rayon de convergence est égal à 1/L.
Par exemple, la série entière
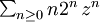 admet un rayon de convergence égal à
admet un rayon de convergence égal à 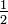 .
.Mais il est souvent plus efficace d'employer les propriétés de convergence pour donner d'autres caractérisations du rayon de convergence. Par exemple, le rayon est la borne supérieure des modules des complexes z pour lesquels la suite de terme général anzn converge vers 0.
Fonction somme
Si
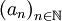 est une suite complexe telle que la série entière
est une suite complexe telle que la série entière 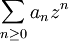 admet un rayon de convergence R strictement positif, on peut alors définir sa fonction somme, en tout point de convergence, par
admet un rayon de convergence R strictement positif, on peut alors définir sa fonction somme, en tout point de convergence, parCette fonction est notamment définie sur le disque de convergence D(0,R).
Il existe une grande variété de comportements possibles pour la série et la fonction somme au bord du domaine de définition. Notamment, la divergence de la série en un point de module R n'est pas incompatible avec l'existence d'une limite en R pour la fonction. Ainsi par somme d'une série géométrique,
La fonction se prolonge par continuité en -1 et 1 qui sont pourtant des valeurs pour lesquelles la série diverge.
Exemples
Une fonction polynôme réelle ou complexe est une série entière de rayon de convergence infini.
La série géométrique
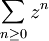 a pour rayon de convergence 1 et sa fonction somme vaut
a pour rayon de convergence 1 et sa fonction somme vaut  sur le disque ouvert D(0,1).
sur le disque ouvert D(0,1).La série entière
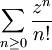 a un rayon de convergence infini. Sa fonction somme, définie dans tout le plan complexe, est appelée fonction exponentielle complexe. C'est à partir d'elle que sont analytiquement définies les fonctions sinus et cosinus.
a un rayon de convergence infini. Sa fonction somme, définie dans tout le plan complexe, est appelée fonction exponentielle complexe. C'est à partir d'elle que sont analytiquement définies les fonctions sinus et cosinus.La série entière
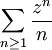 a un rayon de convergence égal à 1. Elle constitue une détermination du logarithme complexe, c'est-à-dire une réciproque d'une restriction de l'exponentielle complexe.
a un rayon de convergence égal à 1. Elle constitue une détermination du logarithme complexe, c'est-à-dire une réciproque d'une restriction de l'exponentielle complexe.Opérations sur les séries entières
Les propriétés qui suivent seront énoncées pour deux séries entières
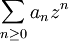 et
et  , de rayons de convergence respectifs R et R′, et dont les fonctions somme s'écrivent
, de rayons de convergence respectifs R et R′, et dont les fonctions somme s'écriventSomme et produit
La somme des séries entières f et g est une série entière. Si R et R′ sont distincts, son rayon est le minimum de R et R′. S'ils sont égaux, elle a un rayon supérieur ou égal à cette valeur commune.
On peut former le produit des deux séries entières, en utilisant les propriétés du produit de Cauchy des séries à termes complexes. Ainsi la série produit se calcule par la formule
Elle admet un rayon de convergence supérieur ou égal au minimum des deux rayons.
Substitution
Sous certaines conditions, il est possible d'effectuer la substitution d'une série entière dans une autre, ce qui conduit à composer les fonctions sommes.
La composition est possible si les rayons de convergence des deux séries sont non nuls, et si le coefficient a0 = f(0) est nul. La série obtenue par substitution est de rayon strictement positif. Sur un disque suffisamment petit inclus dans le disque de convergence, la somme de la série est la composée
 .
.La substitution peut notamment être utilisée pour le calcul, quand il est possible, d'inverse d'une série entière, puis du quotient de deux séries entières.
Dérivation
La série
 est appelée série dérivée de la série
est appelée série dérivée de la série 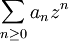 . Une série admet le même rayon de convergence que sa dérivée, et si cette valeur commune est strictement positive, il est possible de dériver terme à terme la série dans le disque de convergence
. Une série admet le même rayon de convergence que sa dérivée, et si cette valeur commune est strictement positive, il est possible de dériver terme à terme la série dans le disque de convergencePour une série entière de la variable réelle, la fonction somme associée est donc dérivable sur ]-R,+R[, et même de classe
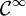 , puisqu'il est possible d'effectuer p dérivation successives terme à terme, toutes les séries dérivées successives ayant même rayon de convergence.
, puisqu'il est possible d'effectuer p dérivation successives terme à terme, toutes les séries dérivées successives ayant même rayon de convergence.Pour une série de la variable complexe, la dérivée est à prendre au sens complexe également, c'est-à-dire que la fonction somme est holomorphe dans le disque de convergence.
Fonction développable en série entière
Une fonction f de la variable réelle ou complexe, définie au voisinage d'un point c, est dite développable en série entière au voisinage de c s'il existe une série entière
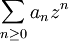 de rayon R strictement positif telle que
de rayon R strictement positif telle que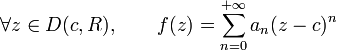 .
.
Au sujet de l'existence et de l'unicité du développement
Une fonction f développable en série entière est nécessairement de classe
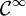 au voisinage de c. Le coefficient d'indice n du développement est donné par la formule
au voisinage de c. Le coefficient d'indice n du développement est donné par la formuleCeci montre que si le développement en série entière existe, il est unique, et donné par la série de Taylor de la fonction au point c.
Il ne suffit pas qu'une fonction soit
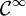 pour qu'elle soit développable en série entière.
pour qu'elle soit développable en série entière.On peut donner comme contre-exemple la fonction définie sur la droite réelle par
 , prolongée par continuité par f(0)=0. En effet cette fonction est dérivable à tout ordre, de dérivée valant 0 à l'origine. Sa série de Taylor en 0 est la série nulle. Elle admet un rayon de convergence infini, mais n'a pour somme f(x) en aucun point autre que 0.
, prolongée par continuité par f(0)=0. En effet cette fonction est dérivable à tout ordre, de dérivée valant 0 à l'origine. Sa série de Taylor en 0 est la série nulle. Elle admet un rayon de convergence infini, mais n'a pour somme f(x) en aucun point autre que 0.Développements usuels en séries entières
Ces développements usuels sont souvent très utiles dans le calcul d'intégrales. Ils sont donnés ici avec indication du rayon de convergence dans le champ complexe ou réel.

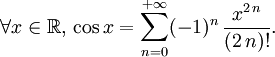
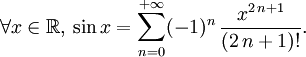
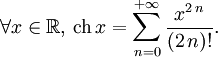

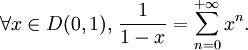
![\forall x\in]-1,1],\, \ln (1+x)=\sum_{n=1}^{+{\infty}}(-1)^{n-1}{x^{n}\over{n}}.](/pictures/frwiki/55/7e7a1193dff73cedef0c5ff515985d9d.png)
![\forall x\in[-1,1],\, \operatorname{Arctan} \,x=\sum_{n=0}^{+{\infty}}(-1)^n\,{\frac{x^{2\,n+1}}{2\,n+1}}\;](/pictures/frwiki/98/bf6d2b531a14df297dc6a79ed7d20b9c.png) , et en particulier,
, et en particulier, 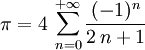 .
.
![\forall x\in\,]-1,1[,\ \forall \alpha\,\not\in\, \mathbb{N},\, (1+x)^\alpha \,=1\;+\;\sum_{n=1}^{+{\infty}}{\frac{\alpha\,(\alpha-1)\ldots(\alpha-n+1)}{n!}\,x^n}.](/pictures/frwiki/101/eafc7c35ab5821a9876be102e2a809b1.png)
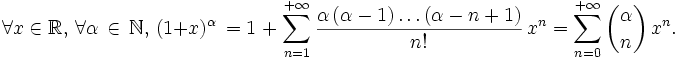
![\forall x\in]-1,1[,\, \operatorname{Argth} \,x=\sum_{n=0}^{+{\infty}}\,{\frac{x^{2\,n+1}}{2\,n+1}}.](/pictures/frwiki/99/ca5f56120e5c0287a906b398ff2095f0.png)
![\forall x\in]-1,1[,\, \operatorname{Arcsin} \,x=\sum_{n=0}^{+{\infty}}\,a_n\,{\frac{x^{2\,n+1}}{2\,n+1}} \quad \text{avec}\; a_n=\left\{\begin{matrix} 1, & \mbox{si }n\mbox{ est nul} \\ \left({\frac{\prod_{k=1}^{n}\,(2\,k-1)}{\prod_{k=1}^{n}\,2\,k}}\right), & \mbox{sinon} \end{matrix}\right.](/pictures/frwiki/97/ad7d3b134f236b315599988b6217045e.png)
![\forall x\in]-1,1[,\, \operatorname{Argsh} \,x=\sum_{n=0}^{+{\infty}}\,(-1)^n\,a_n\,{\frac{x^{2\,n+1}}{2\,n+1}} \quad \mathrm{avec}\; a_n=\left\{\begin{matrix} 1, & \mbox{si }n\mbox{ est nul} \\ \left({\frac{\prod_{k=1}^{n}\,(2\,k-1)}{\prod_{k=1}^{n}\,2\,k}}\right), & \mbox{sinon} \end{matrix}\right.](/pictures/frwiki/51/3c08abf667c210bb579040682da996c4.png)
Remarque : on peut aussi écrire
![\forall x\in\, \left]-\frac{\pi}{2},\frac{\pi}{2}\right[,\, \tan x= \frac{2}{\pi}\, \sum_{n=0}^{+{\infty}}\,{\left({\frac{x}{\pi}}\right)}^{2\,n+1}(2^{2\,n+2}-1)\;\zeta (2\,n+2)\quad \text{avec}\; \forall p>1,\,\zeta(p)=\sum_{n=1}^{+{\infty}}\,\frac{1}{n^p}](/pictures/frwiki/98/b4a54bae6516b9b51c75e8cae348cf5f.png) (fonction zêta de Riemann, dont on connaît, pour tout p entier pair - non nul - une expression explicite sous forme du produit d'un rationnel par une puissance paire de π).
(fonction zêta de Riemann, dont on connaît, pour tout p entier pair - non nul - une expression explicite sous forme du produit d'un rationnel par une puissance paire de π).
Fonctions analytiques
Article détaillé : Fonction analytique.Une fonction de la variable réelle ou complexe, définie sur un ouvert U, est dite analytique sur U lorsqu'elle admet un développement en série entière en tout point de U.
La fonction somme f d'une série entière de rayon de convergence R strictement positif est elle-même analytique sur son disque ouvert de convergence D(0,R). Ceci signifie qu'on peut changer d'origine pour le développement en série entière : précisément, si z0 est un complexe de module strictement inférieur à R, alors f est développable en série entière sur le disque de centre z0 et de rayon R − | z0 | .
Les fonctions analytiques jouissent de propriétés remarquables. Selon le « principe des zéros isolés », les points d'annulation d'une telle fonction sont des points isolés. Le « principe du prolongement analytique » indique que, si deux fonctions analytiques sont définies sur un ouvert connexe U et coïncident sur une partie A incluse dans U présentant au moins un point d'accumulation, alors elles coïncident sur U.
En analyse complexe, on établit que toute fonction holomorphe (c'est-à-dire dérivable au sens complexe) sur un ouvert U est indéfiniment dérivable en tout point par rapport à la variable complexe et est même analytique. Au contraire en analyse réelle, il existe de nombreuses fonctions
 non analytiques.
non analytiques.Comportement au bord du domaine de convergence
Théorème de convergence uniforme d'Abel
Article détaillé : Théorème d'Abel (analyse).Le théorème d'Abel donne une propriété de continuité partielle de la fonction somme lorsqu'il y a convergence de la série entière en un point de son cercle de convergence.
Précisément, soit
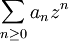 une série entière de rayon de convergence R strictement positif fini. On suppose qu'en un point z0 de module R, la série est convergente. On considère un triangle T ayant pour sommets z0 d'une part et deux points de module strictement inférieur à R d'autre part. Alors la série converge uniformément sur T.
une série entière de rayon de convergence R strictement positif fini. On suppose qu'en un point z0 de module R, la série est convergente. On considère un triangle T ayant pour sommets z0 d'une part et deux points de module strictement inférieur à R d'autre part. Alors la série converge uniformément sur T.Notamment, il y a convergence uniforme sur le segment [0,z0]. Ce cas particulier est appelé théorème d'Abel radial.
Points singuliers et réguliers
Article détaillé : Prolongement analytique.Soit
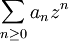 une série entière de rayon de convergence R strictement positif fini, et f la fonction somme. Un point z0 de module R est dit régulier s'il existe un disque ouvert D centré en ce point tel que f se prolonge en une fonction analytique à
une série entière de rayon de convergence R strictement positif fini, et f la fonction somme. Un point z0 de module R est dit régulier s'il existe un disque ouvert D centré en ce point tel que f se prolonge en une fonction analytique à 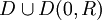 . Dans le cas contraire, le point est dit singulier.
. Dans le cas contraire, le point est dit singulier.Parmi les complexes de module R, il existe toujours un point singulier.
Voir aussi
Rubriques connexes
- Toute fonction développable en série entière est une fonction de classe
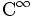 .
. - Une fonction analytique est une fonction développable en série entière au voisinage de tout point.
- Les notions de fonction analytique complexe et de fonction holomorphe coïncident.
- Ces notions nécessitent quelques connaissances en topologie, concernant les ouverts et la connexité.
- Voir également les développements eulériens
Bibliographie
- Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes [détail des éditions]
- Jean Dieudonné, Calcul infinitésimal [détail des éditions]
- Portail des mathématiques
Catégories : Analyse complexe | Série
Wikimedia Foundation. 2010.

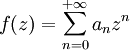
![\forall x \in ]-1,1[,\qquad \frac1{1+x^2}=\sum_{n=0}^{+\infty} (-1)^nx^{2n}.](/pictures/frwiki/102/f1cd26b16c2c7fa6331ca98d31f82695.png)