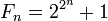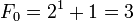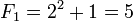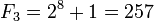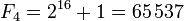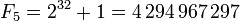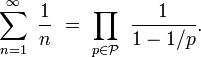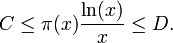- Nombre Premier
-
Nombre premier
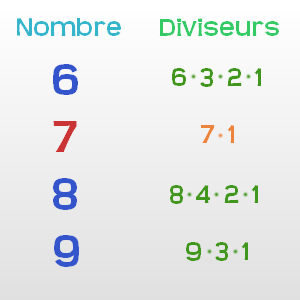 7 est un nombre premier car il admet exactement deux diviseurs positifs.
7 est un nombre premier car il admet exactement deux diviseurs positifs.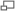
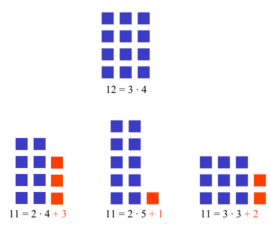
Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Cette définition exclut 1, qui n'a qu'un seul diviseur entier positif. Par opposition, un nombre non nul produit de deux nombres entiers différents de 1 est dit composé. Par exemple 12 = 2 × 6 est composé, tout comme 21 = 3 × 7 ou 7 × 3, mais 11 est premier car 1 et 11 sont les seuls diviseurs de 11. Les nombres 0 et 1 ne sont ni premiers ni composés. Les nombres premiers inférieurs à 100 sont :
De telles listes peuvent être obtenues grâce à diverses méthodes de calcul. On sait depuis l'Antiquité qu'il existe une infinité de nombres premiers. Découvert en 2008, le plus grand nombre premier connu est 243 112 609-1, nombre premier de Mersenne qui comporte près de 13 millions de chiffres en écriture décimale[1].
La notion de nombre premier est une notion de base en arithmétique élémentaire : le théorème fondamental de l'arithmétique assure qu'un nombre composé est factorisable en un produit de nombres premiers, et cette factorisation est unique à l'ordre des facteurs près. Elle admet des généralisations importantes dans des branches des mathématiques plus avancées, comme la théorie algébrique des nombres, qui prennent ainsi à leur tour l'appellation d'arithmétique. Par ailleurs, de nombreuses applications industrielles de l'arithmétique reposent sur la connaissance algorithmique des nombres premiers, et parfois plus précisément sur la difficulté des problèmes algorithmiques qui leur sont liés ; par exemple certains systèmes cryptographiques et des méthodes de transmission de l'information. Les nombres premiers sont aussi utilisés pour construire des tables de hachage et pour constituer des générateurs de nombres pseudo-aléatoires.
Éléments historiques
Les entailles retrouvées sur l’os d'Ishango daté à plus de 20 000 ans avant notre ère, mis au jour par l'archéologue Jean de Heinzelin de Braucourt[2] et antérieur à l'apparition de l'écriture (antérieur à 3 200 ans avant J.-C.), semblent isoler quatre nombres premiers 11, 13, 17 et 19. Certains archéologues l'interprètent comme la preuve de la connaissance des nombres premiers. Toutefois, il existe trop peu de découvertes permettant de cerner les connaissances réelles de cette période ancienne[3].
Des tablettes d'argile séchées attribuées aux civilisations qui se sont succédé en Mésopotamie durant le IIemillénaire av. J.-C. montrent la résolution de problèmes arithmétiques et attestent des premières connaissances de l'époque. Les calculs nécessitaient de connaître des tables d'inverses d'entiers (les réciproques) dont certaines ont été retrouvées. Dans le système sexagésimal utilisé par la civilisation babylonienne pour écrire les entiers, les réciproques des diviseurs des puissances de 60 (nombres réguliers) se calculent facilement : par exemple, diviser par 24, c'est multiplier par
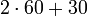 et décaler de deux places le rang. Leur connaissance nécessitait une bonne compréhension de la multiplication, de la division et de la factorisation d'entiers.
et décaler de deux places le rang. Leur connaissance nécessitait une bonne compréhension de la multiplication, de la division et de la factorisation d'entiers.Dans les mathématiques égyptiennes, le calcul fractionnaire demandait des connaissances sur les opérations, les divisions d’entiers et les factorisations. Les Égyptiens ne notaient que les inverses d’entiers (1/2, 1/3, 1/4, 1/5, ...) ; l’écriture des fractions se faisait en additionnant des inverses d'entiers, si possible sans répétition (1/2 + 1/6 au lieu de 1/3 + 1/3). Disposer d’une liste des premiers nombres premiers devait être nécessaire.
La première trace incontestable de la présentation des nombres premiers remonte à l'Antiquité (vers -300 av. J.-C.), et se trouve dans les Éléments d’Euclide (tomes VII à IX). Euclide donne la définition des nombres premiers, la preuve de leur infinité, la définition du plus grand commun diviseur (pgcd) et du plus petit commun multiple (ppcm), et les algorithmes pour les déterminer, aujourd’hui appelés algorithmes d’Euclide. Les connaissances présentées lui sont toutefois bien antérieures.
Structures algébriques, topologiques, et nombres premiers
La notion de nombre premier est liée à l'étude de la structure multiplicative de l'anneau des entiers relatifs. Le théorème fondamental de l'arithmétique, basé sur le lemme d'Euclide, élucide cette structure en assurant que tout entier se factorise en un produit de nombres premiers, de manière unique à l'ordre des facteurs près. Ce théorème permet de déterminer des notions de pgcd, ppcm, et de nombres premiers entre eux, qui sont utiles pour la résolution de certaines équations diophantiennes, notamment la caractérisation des triplets pythagoriciens.
D'autres problèmes naturels sont envisagés, comme la détermination de la proportion d'entiers premiers à un entier fixé. L'introduction de structures algébriques plus avancées permet de résoudre ce problème rapidement dans le cadre de l'arithmétique modulaire. De nombreux théorèmes classiques de nature arithmétique peuvent être énoncés, comme le petit théorème de Fermat, ou le théorème de Wilson ; ou des théorèmes de nature plus algébrique comme le théorème des restes chinois.
Le théorème des restes chinois est un premier résultat dans l'étude des groupes abéliens finis[4]. Il est en fait suffisant pour décrire entièrement la structure de ces groupes, qui est donc en partie liée à la décomposition en produit de facteurs premiers de leurs cardinaux. Les choses sont plus compliquées pour les groupes non abéliens, cependant, l'étude se base à nouveau sur la décomposition en facteurs premiers de leurs cardinaux, à travers la théorie de Sylow.
Les nombres premiers interviennent aussi dans les structures topologiques. Le corps des nombres rationnels admet une structure topologique habituelle, qui donne par complétion le corps des nombres réels. Pour chaque nombre premier p, une autre structure topologique peut être construite, à partir de la norme suivante : si
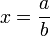 est un nombre rationnel non nul sous forme irréductible et que pα et pβ sont les plus grandes puissances de p divisant a et b, la norme p-adique de x est pβ − α. En complétant le corps des rationnels suivant cette norme, on obtient le corps des nombres p-adiques, introduit par Kurt Hensel au début du XXe siècle. Le théorème d'Ostrowski assure que ces normes p-adiques et la norme habituelle sont les seules sur le corps des nombres rationnels, à équivalence près[5].
est un nombre rationnel non nul sous forme irréductible et que pα et pβ sont les plus grandes puissances de p divisant a et b, la norme p-adique de x est pβ − α. En complétant le corps des rationnels suivant cette norme, on obtient le corps des nombres p-adiques, introduit par Kurt Hensel au début du XXe siècle. Le théorème d'Ostrowski assure que ces normes p-adiques et la norme habituelle sont les seules sur le corps des nombres rationnels, à équivalence près[5].Nombres premiers particuliers
Nombres premiers de Mersenne
Article détaillé : Nombre premier de Mersenne.Les nombres premiers de la forme :
- Mp = 2p − 1
où p est lui-même un nombre premier, sont appelés nombres premiers de Mersenne. Les grands nombres premiers sont souvent recherchés sous cette forme car il existe un test efficace, le test de primalité de Lucas-Lehmer, pour déterminer si un tel nombre est premier ou non.
En 2009, le plus grand nombre premier connu est M43 112 609=243 112 609-1, qui comporte 12 978 189 chiffres en écriture décimale. Il s'agit (chronologiquement) du 45e nombre premier de Mersenne connu et sa découverte a été annoncée le 23 août 2008 grâce aux efforts du projet collaboratif de calcul distribué « Great Internet Mersenne Prime Search ». Le 46e nombre premier de Mersenne, 237 156 667-1, qui est inférieur au précédent a été découvert deux semaines plus tard.
L'Electronic Frontier Foundation offre un prix de calcul coopératif[6] d'un montant de 100 000 USD pour la découverte d'un nombre premier d'au moins 10 millions de chiffres décimaux, afin d'encourager les internautes à contribuer à la résolution de problèmes scientifiques par le calcul distribué.
Nombres premiers jumeaux
Article détaillé : Nombres premiers jumeaux.Deux nombres premiers sont dits jumeaux s'ils ne différent que de deux. Hormis pour la paire (2, 3), cette distance de deux est la plus petite distance possible entre deux nombres premiers. Les plus petits nombres premiers jumeaux sont 3 et 5, 5 et 7, 11 et 13.
Au 15 janvier 2007, les plus grands nombres premiers jumeaux connus sont 2003663613 × 2195000±1, qui possèdent 58 711 chiffres en écriture décimale et furent découverts par Éric Vautier dans le cadre des projets de calcul distribué Twin Prime Search et PrimeGrid[7].
Il est conjecturé qu'il existe une infinité de nombres premiers jumeaux.
Nombres premiers et nombres de Fermat
Article détaillé : Nombre de Fermat.Les nombres premiers de la forme :
sont appelés les nombres premiers de Fermat. Pierre de Fermat avait conjecturé que tous ces nombres devaient être premiers. Cependant, les seuls nombres de Fermat premiers connus sont :
Le nombre de Fermat F5 n’est pas premier : il est divisible par 641.
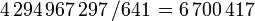
Il s'agit du premier contre-exemple à cette conjecture de Fermat, découvert par Euler en 1732.
Algorithmique : calcul des nombres premiers et tests de primalité
Crible d'Ératosthène et algorithme par essais de division
 Le crible d'Ératosthène : nombres premiers inférieurs à 120.
Le crible d'Ératosthène : nombres premiers inférieurs à 120.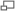
Les premiers algorithmes pour décider si un nombre est premier (appelés tests de primalité) consistent à essayer de le diviser par tous les nombres inférieurs à sa racine carrée : s'il est divisible par l'un d'entre eux, il est composé, et sinon, il est premier. Cependant, l'algorithme déduit de cette formulation peut être rendu plus efficace : il suggère beaucoup de divisions inutiles, par exemple, si un nombre n'est pas divisible par 2, il est inutile de tester s'il est divisible par 4. En fait, il suffit de tester sa divisibilité par tous les nombres premiers inférieurs à sa racine carrée.
Le crible d'Ératosthène est une méthode, reposant sur cette idée, qui fournit la liste des nombres premiers inférieurs à une valeur fixée n (n = 120 dans l'animation ci-contre) :
- On forme la liste des entiers de 2 à n ;
- On retient comme « nombre premier » le premier nombre de la liste non encore barré (le premier dans ce cas est 2) ;
- On barre tous les entiers multiples du nombre retenu à l'étape précédente, en commençant par son carré (puisque 2*i, 3*i, ...(i-1)*i ont déjà été barrés en tant que multiples de 2, 3, ...) ;
- On répète les deux dernières opérations (c'est-à-dire : on retient le prochain nombre non barré et on barre ses multiples) ;
- Dès qu'on en est à chercher les multiples des nombres excédant la racine carrée de n, on termine l'algorithme.
Ainsi les nombres premiers inférieurs à n sont les nombres qui restent non barrés à la fin du processus. Cet algorithme est de complexité algorithmique exponentielle.
Le crible d'Ératosthène fournit donc plus d'information que la seule primalité de n. Si seule cette information est souhaitée, une variante parfois plus efficace consiste à ne tester la divisibilité de n que par des petits nombres premiers dans une liste fixée au préalable (par exemple 2, 3 et 5), puis par tous les nombres entiers inférieurs à la racine carrée de n qui ne sont divisibles par aucun des petits nombres premiers choisis ; cela amène à tester la divisibilité par des nombres non premiers (par exemple 49 si les petits premiers sont 2, 3 et 5 et que n excède 2500), mais un choix d'un nombre suffisant de petits nombres premiers doit permettre de contrôler le nombre de tests inutiles effectués[8].
Autres algorithmes
Une variante du crible d'Ératosthène est le crible de Sundaram qui consiste à former les produits de nombres impairs. Les nombres qui ne sont pas atteints par cette méthode sont les nombres premiers impairs, c'est-à-dire tous les nombres premiers sauf 2. Par ailleurs, à partir du crible d'Ératosthène, la factorisation de l'entier n peut facilement être trouvée. D'autres méthodes plus générales concernant ce problème plus difficile que simplement déterminer la primalité sont aussi appelées méthodes de crible, la plus efficace étant actuellement le crible général des corps de nombres[9].
Les algorithmes présentés précédemment ont une complexité trop importante pour pouvoir être menés à terme, même avec les ordinateurs les plus puissants, quand n devient grand.
Une autre classe d'algorithme consiste à tester l'entier n pour une famille de propriétés vérifiées par les nombres premiers : si une propriété de cette famille n'est pas vérifiée pour n, alors il est composé ; en revanche, le fait qu'une des propriétés de la famille soit vérifiée pour n ne suffit pas à assurer la primalité. Toutefois, si cette famille est telle qu'un nombre composé ne vérifie pas au moins la moitié des propriétés en jeu, alors l'utilisateur peut estimer qu'un nombre n qui vérifie k propriétés de la famille est premier avec une probabilité supérieure à 1-2-k : il est déclaré probablement premier à partir d'une valeur de k à choisir par l'utilisateur ; un nombre déclaré probablement premier, mais qui n'est pas premier est appelé nombre pseudo-premier. Un test basé sur ce principe est appelé test probabiliste de primalité. De tels tests reposent souvent sur le petit théorème de Fermat, amenant au test de primalité de Fermat, et à ses raffinements : le test de primalité de Solovay-Strassen et celui de Miller-Rabin, qui sont des améliorations, car ils admettent moins de nombres pseudo-premiers.[10]
L'algorithme AKS mis au point en 2002 permet de déterminer si un nombre donné N est premier en utilisant un temps de calcul polynomial.
Des formules sur les nombres premiers
Article détaillé : Formule pour les nombres premiers.De nombreuses formules ont été cherchées pour générer les nombres premiers. Le plus haut niveau d'exigence serait de trouver une formule qui à un entier n associe le ne nombre premier. De manière un peu plus souple, on peut se contenter d'exiger une fonction f qui à tout entier n associe un nombre premier et telle que chaque valeur prise ne le soit qu'une fois.
Enfin, on souhaite que la fonction soit calculable en pratique[11]. Par exemple, le théorème de Wilson assure que p est un nombre premier si et seulement si
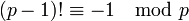 . Il s'ensuit que la fonction
. Il s'ensuit que la fonction  vaut n si n est un nombre premier et vaut 2 sinon. Cependant, le calcul de la factorielle est rédhibitoire, et cette fonction a donc peu de valeur pour générer les nombres premiers.
vaut n si n est un nombre premier et vaut 2 sinon. Cependant, le calcul de la factorielle est rédhibitoire, et cette fonction a donc peu de valeur pour générer les nombres premiers.Il est donc tentant de chercher des fonctions polynômes dont les valeurs sont des nombres premiers. Ceci a conduit au résultat (négatif) suivant: un polynôme, à une ou plusieurs variables, dont les valeurs aux entiers naturels sont des nombres premiers, est un polynôme constant[12].
La recherche de polynômes vérifiant une propriété plus faible s'est développée à partir de la notion d'ensemble diophantien de nombres entiers ; de tels ensembles peuvent être caractérisés comme les ensembles de valeurs strictement positives prises par un polynôme (à plusieurs variables) dont les coefficients et les variables sont des nombres entiers.
Un travail mené dans les années 1960 et 1970, notamment par Putnam, Matijasevic, Davis, Robinson, permet de montrer que l'ensemble des nombres premiers est diophantien, conduisant à l'existence de polynômes à coefficients et variables entières dont toutes les valeurs positives sont les nombres premiers. L'écriture de divers polynômes explicites a ensuite été possible, avec différents nombres de variables, et divers degrés. Notamment, le polynôme suivant, de degré 25 à 26 variables (de a à z), a été déterminé par Jones, Sato, Wada et Wiens en 1976 :
- ( 1
- − [ w.z + h + j − q ]2
- − [ 2.n + p + q + z − e ]2
- − [ a2.y2 − y2 + 1 − x2 ]2
- − [ e3.(e + 2).(a + 1)2 + 1 − o2 ]2
- − [ 16.(k + 1)3.(k + 2).(n + 1)2 + 1 − f2 ]2
- − [ ((a + u2.(u2 − a))2 − 1).(n + 4.d.y)2 + 1 − (x + c.u)2 ]2
- − [ a.i + k + 1 − l − i ]2
- − [ (g.k + 2.g + k + 1).(h + j) + h − z ]2
- − [ 16.r2.y4.(a2 − 1) + 1 − u2 ]2
- − [ p − m + l.(a − n − 1) + b.(2.a.n + 2.a − n2 − 2.n − 2) ]2
- − [ z − p.m + p.l.a − p2l + t.(2.a.p − p2 − 1) ]2
- − [ q − x + y.(a − p − 1) + s.(2.a.p + 2.a − p2 − 2.p − 2) ]2
- − [ a2.l2 − l2 + 1 − m2 ]2
- − [ n + l + v − y ]2
- ) . (k + 2)
De même que pour les formules à factorielles, l'exploitation de ce polynôme ne donne aucun résultat en pratique car il ne donne pratiquement que des valeurs négatives quand on fait varier les variables a à z de 0 à l'infini.
La notion d'ensemble diophantien s'est plus généralement développée à partir des problèmes posés par le dixième problème de Hilbert sur les équations diophantiennes[13].
Répartition des nombres premiers
Infinité des nombres premiers
Euclide a démontré dans ses Éléments (proposition 20 du Livre IX) que les nombres premiers sont en plus grande quantité que toute quantité proposée de nombres premiers. Autrement dit, il existe une infinité de nombres premiers. La démonstration d'Euclide repose sur la constatation qu'une famille finie p1,...,pn de nombres premiers étant donnée, tout nombre premier divisant le produit des éléments de cette famille augmenté de 1 est en dehors de cette famille (et un tel diviseur existe, ce qui est aussi prouvé par Euclide)[14].
D'autres démonstrations de l'infinité des nombres premiers ont été données. La preuve d'Euler[15] utilise l'identité :
Dans la formule précédente, le terme de gauche est la somme de la série harmonique, qui est divergente. Par conséquent, le produit de droite doit contenir une infinité de facteurs.
Furstenberg fournit une preuve utilisant une argumentation topologique[16].
Les avancées du XIXe siècle
 La distribution des nombres premiers de 1 à 76 800, de gauche à droite et de haut en bas. Un pixel noir signifie que le nombre est premier alors qu'un blanc signifie qu'il ne l'est pas.
La distribution des nombres premiers de 1 à 76 800, de gauche à droite et de haut en bas. Un pixel noir signifie que le nombre est premier alors qu'un blanc signifie qu'il ne l'est pas.
Le résultat sur l'infinité des nombres premiers amène des questions plus précises concernant la fonction qui à un nombre réel x associe π(x), le nombre de nombres premiers inférieurs à x, et qui tend donc vers l'infini [17]. Une conjecture importante au XIXe siècle, formulée par Adrien-Marie Legendre et Carl Friedrich Gauss, était que cette fonction de compte des nombres premiers est équivalente à la fonction
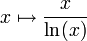 quand x tend vers l'infini, c'est-à-dire que la proportion de nombres premiers parmi les nombres inférieurs à x (soit
quand x tend vers l'infini, c'est-à-dire que la proportion de nombres premiers parmi les nombres inférieurs à x (soit 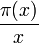 ) tend vers 0 à la vitesse de
) tend vers 0 à la vitesse de 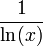 . Avant la démonstration de la conjecture à la fin du siècle, un résultat partiel[18] avait été démontré par Pafnouti Tchebychev, l'existence de deux constantes explicites C et D telles qu'on ait l'encadrement, pour x assez grand :
. Avant la démonstration de la conjecture à la fin du siècle, un résultat partiel[18] avait été démontré par Pafnouti Tchebychev, l'existence de deux constantes explicites C et D telles qu'on ait l'encadrement, pour x assez grand :L'inégalité de Tchebychev permettait notamment de démontrer le postulat de Bertrand selon lequel dans tout intervalle d'entiers naturels entre un entier et son double existe au moins un nombre premier[19]. Plus généralement, les résultats sur la fonction de compte des nombres premiers permettent d'obtenir des résultats sur le ne nombre premier ; par exemple les résultats d'Ishikawa de 1934 sont des conséquences directes des théorèmes de Tchebychev : pn + pn + 1 > pn + 2 et pnpm > pn + m, où pn désigne le ne nombre premier (et donc p1=2) ; ou encore, d'après un résultat de Felgner de 1990 : 0,91 n ln(n) < pn < 1,7 n ln(n)[20].
La démonstration analytique d'Euler sur l'infinité des nombres premiers peut être vue comme un premier pas vers la résolution de problèmes plus avancés. Elle consiste essentiellement à étudier le comportement de la fonction zêta de Riemann en 1 au moyen de ce qu'il est convenu d'appeler un produit eulérien, et d'en déduire la divergence de la série des inverses des nombres premiers. En reprenant cette étude, au moyen d'un outil appelé caractère de Dirichlet, et en utilisant à la place de la fonction zêta de Riemann des fonctions analogues appelées fonction L de Dirichlet, Dirichlet a été capable d'adapter la démonstration aux nombres premiers dans des progressions arithmétiques : si a et b sont premiers entre eux, alors il existe une infinité de nombres premiers de la forme aq+b. Plus précisément, les nombres premiers sont équirépartis entre les différentes progressions arithmétiques de raison a (c'est-à-dire avec a fixé, et b variant parmi les divers restes inversibles dans la division euclidienne par a)[21].
La conjecture de Legendre et Gauss a été démontrée indépendamment par Jacques Hadamard et Charles-Jean de La Vallée Poussin en 1896[22], et porte le nom de théorème des nombres premiers. Ces démonstrations nécessitent des outils puissants d'analyse complexe pour démontrer un énoncé d'arithmétique et d'analyse réelle. Une stratégie pour ces démonstrations est l'étude de la fonction zêta de Riemann sur un domaine plus grand qu'un simple voisinage de 1 : il est nécessaire de la contrôler (c'est-à-dire majorer son module) au voisinage de la droite verticale des nombres de partie réelle 1 dans le plan complexe[23]. En particulier, l'étude de la fonction zêta de Riemann devient un thème central en théorie analytique des nombres, en particulier l'hypothèse de Riemann sur la localisation de ses zéros, encore non démontrée, qui aurait des conséquences fortes sur l'étude de la fonction de compte des nombres premiers. Ultérieurement, des démonstrations ont été proposées sans recours à l'analyse complexe (par Erdös et Selberg au milieu du XXe siècle)[24]. Toutefois, la puissance des outils d'analyse complexe a conduit au développement d'une branche entière des mathématiques : la théorie analytique des nombres.
Théorème de Green-Tao
Un théorème démontré en 2004 par Ben Joseph Green et Terence Tao généralise notamment le théorème de Dirichlet en assurant que pour tout entier k, il existe une infinité de suites de k nombres premiers en progression arithmétique, c'est-à-dire de la forme :
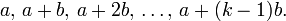
Le théorème de Green-Tao est en fait bien plus fort que cet énoncé seul : par exemple, ils sont en mesure d'affirmer qu'une telle progression arithmétique existe, avec des entiers tous plus petits que :
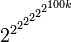
Ils assurent aussi que pour tout entier k et tout réel δ strictement positif, pour tout x suffisamment grand, si P est un ensemble de nombre premiers inférieurs à x contenant au moins δπ(x) éléments, alors P contient au moins une progression arithmétique de nombres premiers comptant k termes[25].
Une conjecture
De nombreux résultats et conjectures sur la répartition des nombres premiers sont contenus dans la conjecture générale suivante. Soit f1,...,fk des polynômes de degré 1, irréductibles et vérifiant la propriété que pour tout nombre premier p il y ait au moins un entier n parmi 0, ..., p-1 tel que p ne divise pas le produit des fi(n). On note ω(p) le complémentaire à p du nombre de tels entiers. Un tel ensemble de polynômes est dit admissible ; on cherche à connaître la proportion d'entiers en lesquels les polynômes prennent simultanément des valeurs premières, et se limiter à des ensembles de polynômes admissibles permet d'éviter des cas triviaux comme f1(t)=t, et f2(t)=t+1. Il est alors conjecturé[26] que le nombre d'entiers n plus petits qu'un réel x tels que les valeurs f1(n),...,fk(n) sont simultanément premières, est, pour x assez grand, de l'ordre de :
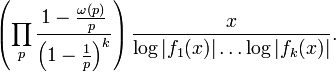
Le théorème des nombres premiers correspond au cas k=1 et ft=t, le théorème de Dirichlet à k=1 et ft=at+b, et pour k=2, f1(t)=t et f2(t)=t+2, on obtient une version quantitative (et donc plus générale) de la conjecture des nombres premiers jumeaux.
Applications
Les nombres premiers, et la théorie des nombres en particulier, ont longtemps été vus comme un sujet purement mathématique, avec peu ou pas d'applications extérieures. Cela changea d'un seul coup dans les années 1970, quand des nouveaux systèmes de cryptographie basés sur les propriétés des nombres premiers furent découverts.
Cryptographie à clé publique
Article détaillé : Cryptographie à clé publique.Jusque dans les années 1970, les systèmes de chiffrement connus étaient basés sur le principe de la cryptographie symétrique, où une même clé (secrète) est utilisée pour chiffrer et déchiffrer un message. En 1978, Ronald Rivest, Adi Shamir et Leonard Adleman décrivent le premier système public de cryptographie asymétrique (nommé d'après eux RSA), basé sur les propriétés des nombres premiers et de la factorisation[27]. Dans un tel système, deux clés sont utilisées : l'une sert à chiffrer, l'autre à déchiffrer. La clé permettant de chiffrer est accompagnée d'un grand nombre entier, le produit de deux grands nombres premiers gardés secrets (de l'ordre de 200 chiffres). Pour calculer la clé de déchiffrement, la seule méthode connue nécessite de connaître les deux facteurs premiers. La sécurité du système est basée sur le fait qu'il est facile de trouver deux grands nombres premiers (en utilisant des tests de primalité) et de les multiplier entre eux, mais qu'il serait difficile pour un attaquant de retrouver ces deux nombres. Ce système permet également de créer des signatures numériques, et a révolutionné le monde de la cryptographie.
Généralisations des nombres premiers
La notion de nombre premier s'est vue généralisée au cours du dix-neuvième siècle dans d'autres structures algébriques que l'anneau des entiers relatifs. Pour résoudre des problèmes arithmétiques tels que le théorème des deux carrés, le théorème des quatre carrés, ou encore la loi de réciprocité quadratique (dont la première preuve est due à Carl Friedrich Gauss dans ses Disquisitiones Arithmeticae), les mathématiciens ont été amenés à mener des raisonnements sur la divisibilité analogues à ceux qui impliquent les nombres entiers dans d'autres anneaux, par exemple celui des entiers de Gauss ou celui des entiers d'Eisenstein.
Le point de vue moderne trouve sa source dans les travaux de Kummer, qui introduit la notion de « nombre premier idéal », dans sa tentative de démontrer le grand théorème de Fermat. Cette notion est à l'origine de la théorie moderne des anneaux d'entiers algébriques, suite aux travaux de Dedekind et Kronecker[28] : en termes modernes, on dit que ces anneaux ont une structure d'anneaux de Dedekind ; notamment, le théorème sur la factorisation des nombres premiers y est remplacé par un résultat de factorisation des idéaux de l'anneau (c'est-à-dire les sous-groupes absorbants pour la multiplication, que Kummer appelait donc « nombres idéaux ») en produit d'idéaux premiers. L'arithmétique dans ces anneaux a en général des liens profonds et difficiles avec l'arithmétique des nombres premiers classiques : par exemple, dans ses travaux sur le théorème de Fermat, Kummer parvient à démontrer l'impossibilité de trouver des solutions non triviales (c'est-à-dire avec x, y et z non nuls) à l'équation xp+yp=zp si p est un nombre premier vérifiant une condition portant sur la nature de l'anneau des entiers algébriques engendré par une racine primitive p-ème de l'unité ; c'est-à-dire si p est ce qu'on appelle un nombre premier régulier.
Questions ouvertes
Il y a beaucoup de questions ouvertes sur les nombres premiers. Par exemple :
- La conjecture de Goldbach : tout nombre pair strictement supérieur à 2 peut-il s'écrire comme somme de deux nombres premiers ?
- La conjecture de De Polignac : tout entier naturel pair peut-il s'écrire comme différence de deux nombres premiers consécutifs et cela d'une infinité de manières?
- Conjecture des nombres premiers jumeaux : un couple de nombres premiers jumeaux est une paire de nombres premiers dont la différence est égale à 2, comme 11 et 13. Existe-t-il une infinité de jumeaux premiers ?
- Toute suite de Fibonacci contient-elle une infinité de nombres premiers ?
- Existe-t-il une infinité de nombres premiers de Fermat ?
- Y a-t-il une infinité de nombres premiers de la forme n² + 1 ?
- Y a-t-il une infinité de nombres premiers factoriels ?
- Y a-t-il une infinité de nombres premiers primoriels ?
- Soit la suite, dite d'Euclide-Mullin, de premier terme u1=2 et telle que le terme un soit le plus petit nombre premier diviseur du produit des termes ui, pour i<n, augmenté de 1. Tous les nombres premiers apparaissent-ils dans cette suite ? C'est une conjecture de Daniel Shanks.
- La conjecture de Legendre affirme qu'il existe un nombre premier entre n² et (n+1)². Cette conjecture non démontrée est liée à l'hypothèse de Riemann et, comme cette dernière, non démontrée.
Références
Notes
- ↑ Nombre découvert le 23 août 2008 par le programme Gimps (Great Internet Mersenne Prime Search)
- ↑ Voir Marcus du Sautoy, La symphonie des nombres premiers P.42
- ↑ Préhistoire de la géométrie : le problème des sources, article d'Olivier Keller.
- ↑ Patrice Naudin, Claude Quitté Algorithmique algébrique [détail des éditions], début du chapitre 3
- ↑ voir le livre (en) Fernando Gouvêa, p-adic Numbers : An Introduction [détail des éditions]
- ↑ prix de calcul coopératif
- ↑ (en) [pdf] Twin Prime Search, Communiqué officiel de la découverte du 15 janvier 2007
- ↑ Voir (en) Henri Cohen, A course in computational algebraic number theory [détail des éditions], début du chapitre 8, notamment l'algorithme 8.1.1.
- ↑ Voir (en) Henri Cohen, A course in computational algebraic number theory [détail des éditions], chapitre 10, plus particulièrement la section 5.
- ↑ voir Patrice Naudin, Claude Quitté Algorithmique algébrique [détail des éditions], chapitre 4, section 6, ou (en) Henri Cohen, A course in computational algebraic number theory [détail des éditions], chapitre 8, section 2
- ↑ Introduction du chapitre 3 du livre de Ribenboim The new book of prime number records.
- ↑ Chapitre 3, section II du livre de Ribenboim The new book of prime number records.
- ↑ Chapitre 3 section III du livre de Ribenboim The new book of prime number records.
- ↑ (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions] Section 2.1.
- ↑ (la) Léonard Euler, Variae observationes circa series infinitas, Commentarii academiae scientiarum Petropolitanae 9, (1744), 160-188, ou Opera Omnia, Series 1, Volume 14, 217 - 244. Téléchargeable à [1]. L'identité y est le théorème 7, p. 172 et l'infinité des nombres premiers y est implicitement rappelée et analysée dans les corollaires qui suivent.
- ↑ (en) Voir le livre de Ribenboim, The new book of prime number records, qui recense par ailleurs de nombreuses autres preuves
- ↑ (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions] Section 2.1
- ↑ Livre de Ribenboim, chapitre 4, section I.
- ↑ (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions] Chapitre 22, sections 1 à 4.
- ↑ Livre de Ribenboim, chapitre 4, section II, A.
- ↑ (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions] Théorème 15. William John Ellison, en collaboration avec Michel Mendès France, Les nombres premiers [détail des éditions] Chapitre 7.
- ↑ William John Ellison, en collaboration avec Michel Mendès France, Les nombres premiers [détail des éditions] Chapitre 2, section 1.2
- ↑ William John Ellison, en collaboration avec Michel Mendès France, Les nombres premiers [détail des éditions] Chapitre 2, théorème 2.4, puis section 4.
- ↑ William John Ellison, en collaboration avec Michel Mendès France, Les nombres premiers [détail des éditions] Chapitre 2, section 1.2
- ↑ (en) Document de vulgarisation dû à Andrew Granville, qui contient de nombreuses autres conséquences amusantes du résultat de Green et Tao.
- ↑ (en) Document dû à Andrew Granville, page 13, item (15).
- ↑ (en) Ronald Rivest, Adi Shamir et Leonard Adleman, « A Method for Obtaining Digital Signatures and Public-Key Cryptosystems », dans Communications of the ACM, vol. 21, no 2, 1978, p. 120-126 [texte intégral]
- ↑ Eléments d'histoire des mathématiques. Nicolas Bourbaki. Chapitre Algèbre commutative. Théorie des nombres algébriques.
Bibliographie
- (en) Henri Cohen, A course in computational algebraic number theory [détail des éditions] Référence moderne sur les méthodes effectives en théorie des nombres.
- Jean-Paul Delahaye, Merveilleux nombres premiers, Éditions Belin - Pour la Science, 2000 (ISBN 2701150175)
- Michel Demazure, Cours d'algèbre. Primalité, divisibilité, codes, Cassini, 1997. Ce livre contient de nombreux algorithmes écrits en Caml Light.
- William John Ellison, en collaboration avec Michel Mendès France, Les nombres premiers [détail des éditions] Livre très clair, comme introduction à la théorie analytique des nombres.
- (en) Fernando Gouvêa, p-adic Numbers : An Introduction [détail des éditions] Introduction aux nombres p-adiques à la portée d'un large public, tournée vers des objectifs analytiques.
- (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions] Un grand classique d'introduction à la théorie des nombres, qui couvre les sujets de base (congruences), introduit les méthodes algébriques par l'exemple (entiers de Gauss, de Kronecker), et donne une démonstration du théorème des nombres premiers.
- (en) Paulo Ribenboim, The new book of big prime number records, Springer, 1996 (ISBN 0387944575)
- Gérald Tenenbaum et Michel Mendès-France, Les Nombres Premiers, Que sais-je ? n° 571, PUF, 2000 (ISBN 2130483992), 1ère éd. 1997.
Ce dernier ouvrage a fait l'objet de diverses éditions, historiquement:
- Émile Borel, Les Nombres Premiers, Que sais-je ? n° 571, PUF, 1ère éd. 1953
- Jean Itard, Les Nombres Premiers, Que sais-je ? n° 571, PUF, 1ère éd. 1969
Voir aussi
- Théorème des nombres premiers
- Théorème de Wilson
- Crible d'Ératosthène
- Test de primalité
- Liste de nombres premiers
Liens externes
- (en) Page d'Andrew Granville. La partie « Expository lectures » a été en particulier utilisée.
- (en) [2] Page des nombres premiers sur l'encyclopédie électronique des suites entières.
- (fr) Une grande liste des nombres premiers (jusqu'à 1 000 000 000)
- Portail des mathématiques
Catégories : Arithmétique élémentaire | Nombre premier
Wikimedia Foundation. 2010.